题目内容
(2012•海淀区一模)已知函数f(x)=alnx-
x2+
(a∈R且a≠0).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)是否存在实数a,使得对任意的x∈[1,+∞),都有f(x)≤0?若存在,求a的取值范围;若不存在,请说明理由.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)是否存在实数a,使得对任意的x∈[1,+∞),都有f(x)≤0?若存在,求a的取值范围;若不存在,请说明理由.
分析:(Ⅰ)确定函数f(x)的定义域,求导函数,对a分类讨论,利用导数的正负,即可求得f(x)的单调区间;
(Ⅱ)对任意的x∈[1,+∞),都有f(x)≤0,即使得对任意的x∈[1,+∞),都有f(x)max≤0,因此求出函数的最大值,即可确定a的取值范围.
(Ⅱ)对任意的x∈[1,+∞),都有f(x)≤0,即使得对任意的x∈[1,+∞),都有f(x)max≤0,因此求出函数的最大值,即可确定a的取值范围.
解答:解:(Ⅰ)f(x)的定义域为(0,+∞).求导函数可得f′(x)=
-x=
.…(2分)
当a<0时,在区间(0,+∞)上,f'(x)<0.
所以f(x)的单调递减区间是(0,+∞).…(3分)
当a>0时,令f'(x)=0得x=
或x=-
(舍).
函数f(x),f'(x)随x的变化如下:
所以 f(x)的单调递增区间是(0,
),单调递减区间是(
,+∞).…(6分)
综上所述,当a<0时,f(x)的单调递减区间是(0,+∞);
当a>0时,f(x)的单调递增区间是(0,
),单调递减区间是(
,+∞).
(Ⅱ)由(Ⅰ)可知:
当a<0时,f(x)在[1,+∞)上单调递减,所以f(x)在[1,+∞)上的最大值为f(1)=0,即对任意的x∈[1,+∞),都有f(x)≤0.…(7分)
当a>0时,
①当
≤1,即0<a≤1时,f(x)在[1,+∞)上单调递减,所以f(x)在[1,+∞)上的最大值为f(1)=0,即对任意的x∈[1,+∞),都有f(x)≤0.…(10分)
②当
>1,即a>1时,f(x)在[1,
)上单调递增,所以 f(
)>f(1).
又 f(1)=0,所以 f(
)>0,与对于任意的x∈[1,+∞),都有f(x)≤0矛盾.…(12分)
综上所述,存在实数a满足题意,此时a的取值范围是(-∞,0)∪(0,1].…(13分)
| a |
| x |
| -x2+a |
| x |
当a<0时,在区间(0,+∞)上,f'(x)<0.
所以f(x)的单调递减区间是(0,+∞).…(3分)
当a>0时,令f'(x)=0得x=
| a |
| a |
函数f(x),f'(x)随x的变化如下:
| x | (0,
|
|
(
| ||||||
| f'(x) | + | 0 | - | ||||||
| f(x) | ↗ | 极大值 | ↘ |
| a |
| a |
综上所述,当a<0时,f(x)的单调递减区间是(0,+∞);
当a>0时,f(x)的单调递增区间是(0,
| a |
| a |
(Ⅱ)由(Ⅰ)可知:
当a<0时,f(x)在[1,+∞)上单调递减,所以f(x)在[1,+∞)上的最大值为f(1)=0,即对任意的x∈[1,+∞),都有f(x)≤0.…(7分)
当a>0时,
①当
| a |
②当
| a |
| a |
| a |
又 f(1)=0,所以 f(
| a |
综上所述,存在实数a满足题意,此时a的取值范围是(-∞,0)∪(0,1].…(13分)
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,解题的关键是正确求导,合理分类,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
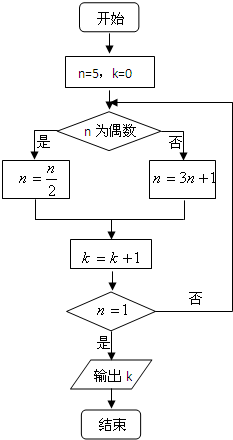 (2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )
(2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )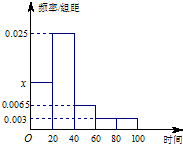 (2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].