题目内容
若抛物线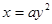
的离心率
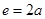，则该抛物线准线方程是（ ）
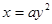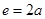的离心率，则该抛物线准线方程是（ ）A． | B． | C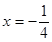． | D． |
B
由抛物线的离心率为1可得
，所以
；抛物线的方程为
，开口向右， 
，准线方程是
.
，所以；抛物线的方程为，开口向右， ，准线方程是.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
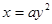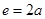的离心率，则该抛物线准线方程是（ ）| A． | B． | C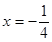． | D． |
，所以；抛物线的方程为，开口向右， ，准线方程是.阅读快车系列答案
的焦点为
，准线为
，过抛物线
上的点
作准线
，若
与
（其中
为坐标原点）的面积之比为
，则点
过抛物线
的焦点
，且与抛物线交于
两点，若线段
的中点到
轴的距离是
，则
__ ▲ __.
的焦点坐标为( ▲ ) 
，求抛物线的方程.
与直线
交于A、B两点，O为坐标原点．
是该抛物线的准线．对于任意实数k，
？如果存在，求出点D的坐标；如不存在，说明理由． 
相切,点C在
上.
的直线与曲线交于A、B两点.问直线
是以
为直角的直角三角形？如果存在，求出点C的坐标;若不能,请说明理由.
( )
