题目内容
8.已知抛物线C:y2=4x的焦点为F,点K是C的准线l和x轴的交点,P在C上运动,则满足条件$\overrightarrow{FM}$=$\overrightarrow{FK}$+$\overrightarrow{FP}$的动点M的轨迹方程是y2=4(x+2).分析 由抛物线的方程求出其准线方程和焦点坐标,进一步得到K的坐标,设出M和P的坐标,由向量等式把P的坐标用M的坐标表示,代入抛物线方程得答案.
解答 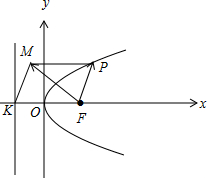 解:如图,
解:如图,
由抛物线C:y2=4x,得2p=4,p=2,$\frac{p}{2}=1$,
∴其准线方程为x=-1,则K(-1,0),F(1,0),
设M(x,y),P(x0,y0),
∴$\overrightarrow{FM}=(x-1,y),\overrightarrow{FK}=(-2,0)$,$\overrightarrow{FP}=({x}_{0}-1,{y}_{0})$,
由$\overrightarrow{FM}$=$\overrightarrow{FK}$+$\overrightarrow{FP}$,得(x-1,y)=(-2,0)+(x0-1,y0)=(x0-3,y0),
∴$\left\{\begin{array}{l}{x-1={x}_{0}-3}\\{y={y}_{0}}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}_{0}=x+2}\\{{y}_{0}=y}\end{array}\right.$,
代入y2=4x,得y2=4(x+2).
∴动点M的轨迹方程是y2=4(x+2).
故答案为:y2=4(x+2).
点评 本题考查了抛物线的简单几何性质,考查了向量的坐标运算,训练了代入法求轨迹方程,是中档题.

练习册系列答案
相关题目
13.若函数y=f(x)(x∈R)满足f(x)+f′(x)>0则下列结论正确的是( )
| A. | e2f(1)>f(-1) | B. | e2f(1)<f(-1) | C. | ef(1)>f(-1) | D. | ef(1)<f(-1) |