题目内容
已知P点为抛物线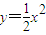 上的任意一点,F点坐标为(0,
上的任意一点,F点坐标为(0, ),则以PF为直径的圆必定( )
),则以PF为直径的圆必定( )A.与x轴相切
B.与y轴相切
C.与y=-
 相切
相切D.与
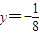 相切
相切
【答案】分析:由题意通过P所在的特殊位置,判断圆与x轴y轴,y=- ,
, 的位置关系,得到选项即可.
的位置关系,得到选项即可.
解答:解:因为P点为抛物线 上的任意一点,F点坐标为(0,
上的任意一点,F点坐标为(0, ),
),
不妨令P在(0,0)点,显然以PF为直径的圆,与y轴相交,与y=- ,
, 相离,
相离,
此时以PF为直径的圆必定与x轴相切.
故选A.
点评:本题考查直线与圆的位置关系,题目考查的是一般性结论,利用特殊点求解,解答简洁,值得同学们学习.
 ,
, 的位置关系,得到选项即可.
的位置关系,得到选项即可.解答:解:因为P点为抛物线
 上的任意一点,F点坐标为(0,
上的任意一点,F点坐标为(0, ),
),不妨令P在(0,0)点,显然以PF为直径的圆,与y轴相交,与y=-
 ,
, 相离,
相离,此时以PF为直径的圆必定与x轴相切.
故选A.
点评:本题考查直线与圆的位置关系,题目考查的是一般性结论,利用特殊点求解,解答简洁,值得同学们学习.

练习册系列答案
相关题目
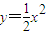 上的任意一点,F点坐标为(0,
上的任意一点,F点坐标为(0, ),则以PF为直径的圆必定( )
),则以PF为直径的圆必定( ) 相切
相切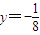 相切
相切