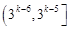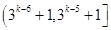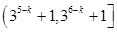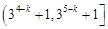题目内容
已知函数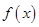 是R上的奇函数,若对于
是R上的奇函数,若对于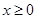 ,都有
,都有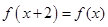 ,
, 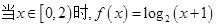 时,
时,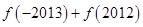 的值为
的值为
A.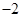 | B.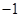 | C.1 | D.2 |
B
解析试题分析:根据函数的奇偶性可得f(-2013)=-f(2013),根据函数的周期性可得f(2012)=f(0),f(2013)=f(1),结合x∈[0,2)时,f(x)=log2(x+1),代入可得答案.解:∵函数f(x)是定义在R上的奇函数,∴f(-2013)=-f(2013),又∵x≥0,都有f(x+2)=f(x),,故f(2012)=f(0),f(2013)=f(1),又由当x∈[0,2)时,f(x)=log2(x+1),,∴f(2012)+f(-2013)=f(2012)-f(2013)=f(0)-f(1)=log21-log22=0-1=-1,故选C
考点:对数函数图象与性质
点评:本题考查的知识点是对数函数图象与性质的综合应用,函数奇偶性的性质,其中熟练掌握函数的奇偶性和周期性是解答的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若定义运算: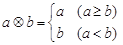 ,例如
,例如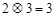 ,则下列等式不能成立的是( )
,则下列等式不能成立的是( )
A.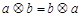 | B.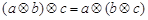 |
C.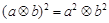 | D.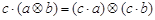 ( (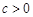 ) ) |
若函数 在区间
在区间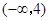 上是增函数,则有( )
上是增函数,则有( )
A. | B.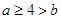 | C.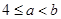 | D. |
下列函数中,既是偶函数又在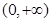 单调递增的函数是( )
单调递增的函数是( )
A.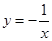 | B.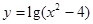 | C.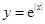 | D.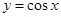 |
偶函数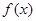 满足
满足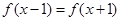 ,当
,当 时,
时, 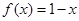 ,则关于
,则关于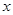 的方程
的方程 在
在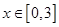 上解的个数是( )
上解的个数是( )
| A.1 | B.2 | C.3 | D.4 |
下列各组函数中表示同一函数的是 ( )
A.f(x)=x与g(x)=( )2 )2 | B.f(x)=|x|与g(x)= |
C.f(x)=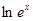 与g(x)= 与g(x)= | D.f(x)= 与g(t)=t+1(t≠1) 与g(t)=t+1(t≠1) |
设f(x)是以2为周期的奇函数,且f(-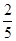 )=3,若sinα=
)=3,若sinα=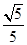 ,则f(4cos2α)= ( )
,则f(4cos2α)= ( )
| A.-3 | B.3 | C.-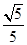 | D.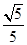 |
已知函数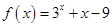 的零点为
的零点为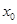 , 则
, 则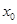 所在区间为( )
所在区间为( )
A. | B.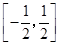 | C.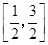 | D.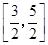 |
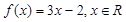 规定:给出一个实数
规定:给出一个实数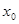 ,赋值
,赋值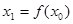 ,若
,若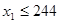 ,则继续赋值
,则继续赋值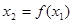 , ,
, , 以此类推,若
以此类推,若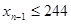 ,则
,则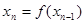 ,否则停止赋值,如果得到
,否则停止赋值,如果得到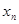 称为赋值了
称为赋值了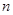 次
次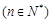 .已知赋值了
.已知赋值了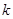 次后停止,则
次后停止,则