题目内容
 如图A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(
如图A,B是单位圆O上的动点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(| 3 | 5 |
(1)求tanα及cos2α.
(2)求B的坐标.
分析:(1)根据三角函数的定义求出sinα和cosα,然后根据三角函数的关系式即可求解.
(2)根据两角和的正弦公式和余弦公式进行求解即可.
(2)根据两角和的正弦公式和余弦公式进行求解即可.
解答:解:(1)∵∠COA=α,A点的坐标为(
,y).
∴cosα=
,
∵A,B分别在第一,二象限.
∴sinα=
.
则tanα=
=
=
,cos2α=2cos2α-1=2×(
)2-1=
-1=-
.
(2)∵△AOB为正三角形,
∴∠COB=α+60°,
设B(x,y),
则y=sin(α+60°)=sin?αcos?60?+cos?αsin?60?=
×
+
×
=
.
x=cos(α+60°)=cos?αcos?60?-sin?αsin?60?=
×
-
×
=
,
即B(
,
).
| 3 |
| 5 |
∴cosα=
| 3 |
| 5 |
∵A,B分别在第一,二象限.
∴sinα=
| 4 |
| 5 |
则tanα=
| sinα |
| cosα |
| ||
|
| 4 |
| 3 |
| 3 |
| 5 |
| 18 |
| 25 |
| 7 |
| 25 |
(2)∵△AOB为正三角形,
∴∠COB=α+60°,
设B(x,y),
则y=sin(α+60°)=sin?αcos?60?+cos?αsin?60?=
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
4+3
| ||
| 10 |
x=cos(α+60°)=cos?αcos?60?-sin?αsin?60?=
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| ||
| 2 |
3-4
| ||
| 10 |
即B(
3-4
| ||
| 10 |
4+3
| ||
| 10 |
点评:本题主要考查三角函数的定义以及两角和的正弦和余弦公式,考查学生的计算能力.

练习册系列答案
相关题目
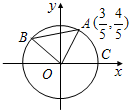 如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为
如图A,B是单位圆O上的点,且B在第二象限. C是圆与x轴正半轴的交点,A点的坐标为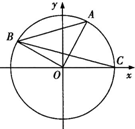 如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为
如图A.B是单位圆O上的点,且点B在第二象限. C是圆O与x轴正半轴的交点,A点的坐标为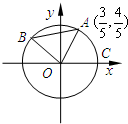 如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为(
如图A、B是单位圆O上的点,且B在第二象限.C是圆与x轴正半轴的交点,A点的坐标为( 如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(
如图A,B是单位圆O上的点,且A,B分别在第一,二象限.C是圆与x轴正半轴的交点,△AOB为正三角形.若A点的坐标为(