题目内容
 已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN=
已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN=| 2 |
| 3 |
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c=
| 3 |
分析:(Ⅰ)由题意可得 a=c-4、b=c-2.又因∠MCN=
π,cosC=-
,可得
=-
,恒等变形得 c2-9c+14=0,再结合c>4,可得c的值.
(Ⅱ)在△ABC中,由正弦定理可得AC=2sinθ,BC=2sin(
-θ).△ABC的周长f(θ)=|AC|+|BC|+|AB|=2sin(θ+
)+
.再由θ∈(0,
),利用正弦函数的定义域和值域,求得f(θ)取得最大值.
| 2 |
| 3 |
| 1 |
| 2 |
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
(Ⅱ)在△ABC中,由正弦定理可得AC=2sinθ,BC=2sin(
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
解答:解:(Ⅰ)∵a、b、c成等差,且公差为2,∴a=c-4、b=c-2.
又∵∠MCN=
π,cosC=-
,
∴
=-
,∴
=-
,
恒等变形得 c2-9c+14=0,解得c=7,或c=2.
又∵c>4,∴c=7.…(6分)
(Ⅱ)在△ABC中,由正弦定理可得
=
=
,
∴
=
=
=2,AC=2sinθ,BC=2sin(
-θ).
∴△ABC的周长f(θ)=|AC|+|BC|+|AB|=2sinθ+2sin(
-θ)+
=2[
sinθ+
cosθ]+
=2sin(θ+
)+
,…(10分)
又∵θ∈(0,
),∴
<θ+
<
,
∴当θ+
=
,即θ=
时,f(θ)取得最大值2+
. …(12分)
又∵∠MCN=
| 2 |
| 3 |
| 1 |
| 2 |
∴
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
| (c-4)2+(c-2)2-c2 |
| 2(c-4)(c-2) |
| 1 |
| 2 |
恒等变形得 c2-9c+14=0,解得c=7,或c=2.
又∵c>4,∴c=7.…(6分)
(Ⅱ)在△ABC中,由正弦定理可得
| AC |
| sin∠ABC |
| BC |
| sin∠BAC |
| AB |
| sin∠ACB |
∴
| AC |
| sinθ |
| BC | ||
sin(
|
| ||
sin
|
| π |
| 3 |
∴△ABC的周长f(θ)=|AC|+|BC|+|AB|=2sinθ+2sin(
| π |
| 3 |
| 3 |
=2[
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
又∵θ∈(0,
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当θ+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| 3 |
点评:本题主要考查正弦定理、余弦定理的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
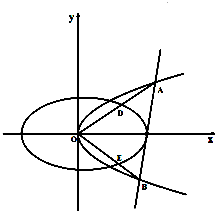 已知椭圆
已知椭圆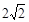 个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?