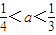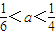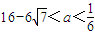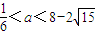题目内容
已知a,b,c是正实数,且ab+bc+ac=1,则abc的最大值为( )
分析:由题意可得
=
≥
,即(abc)2≤
,由此求得abc的最大值.
| 1 |
| 3 |
| ab+bc+ca |
| 3 |
| 3 | (abc)2 |
| 1 |
| 27 |
解答:解:∵a,b,c是正实数,且ab+bc+ac=1,∴
=
≥
,
∴(abc)2≤
,∴abc≤
,即 abc的最大值为
,
故选A.
| 1 |
| 3 |
| ab+bc+ca |
| 3 |
| 3 | (abc)2 |
∴(abc)2≤
| 1 |
| 27 |
| ||
| 9 |
| ||
| 9 |
故选A.
点评:本题主要考查平均值不等式的应用,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目

 ,关于方程
,关于方程 (
( 为正实数)的根的叙述有下列四个命题
为正实数)的根的叙述有下列四个命题 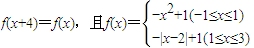 ,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )
,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )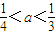
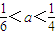
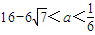
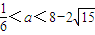
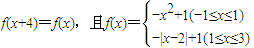 ,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )
,若方程f(x)-ax=0有5个实根,则正实数a的取值范围是( )