题目内容
（2012•卢湾区二模）已知向量
，
的夹角为
，
=4，
=1，若点M在直线OB上，则|
-
|的最小值为
| OA |
| OB |
| π |
| 3 |
| | OA| |
| | OB| |
| OA |
| OM |
2
| 3 |
2
．| 3 |
分析：利用向量的减法运算，结合图象，可知AM⊥OB时，|
-
|取得最小值，由此可得结论．
| OA |
| OM |
解答：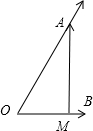
解：由题意
-
=
，
∵点M在直线OB上，
∴当且仅当AM⊥OB时，
最小，即|
-
|取得最小值
∵向量
，
的夹角为
，|
|=4
∴|
-
|的最小值为4sin
=2
故答案为：2
解：由题意| OA |
| OM |
| MA |
∵点M在直线OB上，
∴当且仅当AM⊥OB时，
| MA |
| OA |
| OM |
∵向量
| OA |
| OB |
| π |
| 3 |
| OA |
∴|
| OA |
| OM |
| π |
| 3 |
| 3 |
故答案为：2
| 3 |
点评：本题考查向量知识的运用，考查学生分析解决问题的能力，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目