题目内容
(本题满分12分)
在等差数列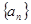 中,
中,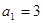 ,其前
,其前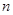 项和为
项和为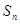 ,等比数列
,等比数列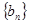 的各项均为正数,
的各项均为正数,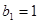 ,公比为
,公比为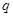 ,且
,且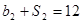 ,
,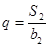 .(Ⅰ)求
.(Ⅰ)求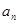 与
与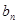 ;(Ⅱ)设数列
;(Ⅱ)设数列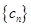 满足
满足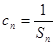 ,求
,求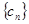 的前
的前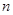 项和
项和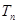 .
.
在等差数列
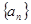 中,
中,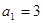 ,其前
,其前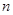 项和为
项和为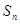 ,等比数列
,等比数列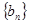 的各项均为正数,
的各项均为正数,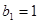 ,公比为
,公比为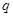 ,且
,且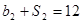 ,
,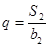 .(Ⅰ)求
.(Ⅰ)求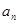 与
与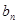 ;(Ⅱ)设数列
;(Ⅱ)设数列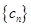 满足
满足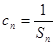 ,求
,求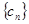 的前
的前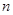 项和
项和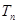 .
.(Ⅰ) ,
, .
.

 ,
, .
. 
本试题主要是考查了等差数列和等比数列的通项公式的求解和数列求和的综合运用。
(1)因为等差数列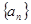 中,
中,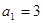 ,其前
,其前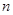 项和为
项和为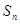 ,等比数列
,等比数列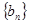 的各项均为正数,
的各项均为正数,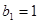 ,公比为
,公比为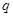 ,且
,且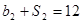 ,
,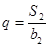 .,利用首项和公差或者公比,表示得到结论。
.,利用首项和公差或者公比,表示得到结论。
(2)在第一问的基础上得到前n项和,然后裂项的思想求解数列的和。
解:(Ⅰ)设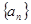 的公差为
的公差为 ,
,
因为 所以
所以 解得
解得 或
或 (舍),
(舍), .
.
故 ,
, .
.

(1)因为等差数列
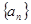 中,
中,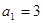 ,其前
,其前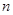 项和为
项和为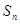 ,等比数列
,等比数列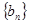 的各项均为正数,
的各项均为正数,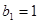 ,公比为
,公比为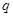 ,且
,且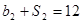 ,
,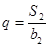 .,利用首项和公差或者公比,表示得到结论。
.,利用首项和公差或者公比,表示得到结论。(2)在第一问的基础上得到前n项和,然后裂项的思想求解数列的和。
解:(Ⅰ)设
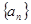 的公差为
的公差为 ,
,因为
 所以
所以 解得
解得 或
或 (舍),
(舍), .
.故
 ,
, .
.

练习册系列答案
相关题目
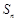 是等差数列{
是等差数列{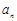 }的前n项和,且
}的前n项和,且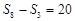 ,则
,则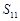 的值为
的值为 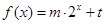 的图像经过点A(0,0),B(3,7)及C
的图像经过点A(0,0),B(3,7)及C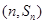 ,
,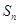 为数列
为数列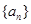 的前n项和
的前n项和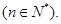
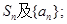
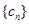 满足
满足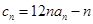 ,求数列
,求数列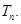
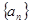 中,
中,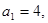
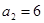 ,且
,且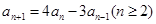
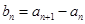 ,求数列
,求数列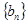 的通项公式;
的通项公式;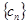 中,
中,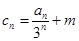 ,且
,且 的值及
的值及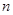 项和.
项和.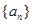 为等比数列,其前
为等比数列,其前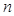 项和为
项和为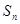 ,已知
,已知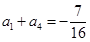 ,且对于任意的
,且对于任意的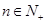 有
有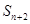 ,
,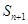 成等差;
成等差;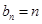 (
(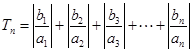 ,若
,若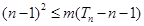 对于
对于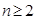 恒成立,求实数
恒成立,求实数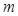 的范围.
的范围.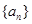 的前n项和为
的前n项和为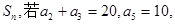 则S5等于
则S5等于 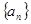 的前
的前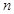 项和分别为
项和分别为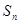 ,若
,若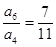 ,则
,则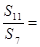 ( )
( )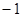
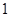
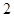

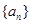 为等差数列,且
为等差数列,且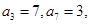 则
则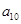 等于( )
等于( )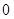
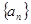 的前
的前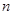 项和
项和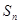 满足:对于任意
满足:对于任意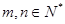 ,都有
,都有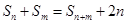 ;若
;若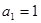 ,则
,则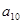 = .
= .