题目内容
边长为1的等边△AOB，O为原点，AB⊥x轴，以O为顶点且过A、B的抛物线方程是（ ）A.y2=
xB.y2=-
x
C.y2=±
xD.y2=±
x
解析:∵△AOB为边长等于1的正三角形，
∴O到AB的距离为，A或B到x轴的距离为.
当抛物线的焦点在x轴的正半轴上时，
设抛物线的方程为y2=2px(p＞0)
∵抛物线过点(，)，
∴(
)2=2p·
.
∴2p=
∴抛物线的方程为y2=
x
当抛物线的焦点在x轴的负半轴上时，
设抛物线的方程为y2=-2px(p＞0)
∵抛物线过点(-
，
)，
∴(
)2=-2p·(-
).∴2p=
∴抛物线的方程为y2=-
x
答案: C
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
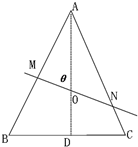如图点O是边长为1的等边三角形ABC的边BC中线AD上一点，且|AO|=2|OD|，过O的直线交边AB于M，交边AC于N，记∠AOM=θ，