题目内容
已知椭圆 (a>b>0)的右焦点为F2(3,0),离心率为e=
(a>b>0)的右焦点为F2(3,0),离心率为e= .
.
(I)求椭圆的方程;
(Ⅱ)设直线经过点P(1,2),与椭圆相交于A,B两点,AB的中点为M,求M的轨迹方程.
解:(Ⅰ)由题意得c=3, =
= ,∴a=2
,∴a=2
结合a2=b2+c2,解得a2=12,b2=3.
所以,椭圆的方程为 ;
;
(Ⅱ)设A(x1,y1),B(x2,y2),M(x,y),则
 ,
,
两方程相减可得
∴ =-
=-
∵直线经过点P(1,2),
∴- =
=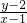
∴x(x-1)+4y(y-2)=0
即M的轨迹方程为x(x-1)+4y(y-2)=0.
分析:(Ⅰ)由题意得c=3, =
= ,由此可得椭圆的方程;
,由此可得椭圆的方程;
(Ⅱ)利用点差法,结合直线的斜率,即可求M的轨迹方程.
点评:本题考查椭圆方程的求法和直线与椭圆位置关系的综合运用,考查点差法的运用,属于中档题.
 =
= ,∴a=2
,∴a=2
结合a2=b2+c2,解得a2=12,b2=3.
所以,椭圆的方程为
 ;
;(Ⅱ)设A(x1,y1),B(x2,y2),M(x,y),则
 ,
,
两方程相减可得

∴
 =-
=-
∵直线经过点P(1,2),
∴-
 =
=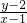
∴x(x-1)+4y(y-2)=0
即M的轨迹方程为x(x-1)+4y(y-2)=0.
分析:(Ⅰ)由题意得c=3,
 =
= ,由此可得椭圆的方程;
,由此可得椭圆的方程;(Ⅱ)利用点差法,结合直线的斜率,即可求M的轨迹方程.
点评:本题考查椭圆方程的求法和直线与椭圆位置关系的综合运用,考查点差法的运用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.