题目内容
17.椐统计,某食品企业一个月内被消费者投诉的次数为0,1,2的概率分别为0.3,0.5,0.2.(Ⅰ)求该企业在一个月内共被消费者投诉不超过1次的概率;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
分析 本题考查的知识点是相互独立事件的概率乘法公式.
(1)设事件A表示“一个月内被投诉的次数为0”,事件B表示“一个月内被投诉的次数为1”,由一个月内被消费者投诉的次数为0,1的概率分别为0.3,0.5,则该企业在一个月内共被消费者投诉不超过1次的概率P=P(A+B)=P(A)+P(B),代入即可求出答案.
(2)设事件Ai表示“第i个月被投诉的次数为0”,事件Bi表示“第i个月被投诉的次数为1”,事件Ci表示“第i个月被投诉的次数为2”,事件D表示“两个月内被投诉2次”,该企业在这两个月内共被消费者投诉2次的概率.P(D)=P(A1C2+A2C1)+P(B1B2)=P(A1C2)+P(A2C1)+P(B1B2),代入数据运算后,易得最终答案.
解答 解:(Ⅰ)设事件A表示“一个月内被投诉的次数为0”,
事件B表示“一个月内被投诉的次数为1”
所以P(A+B)=P(A)+P(B)=0.3+0.5=0.8
(Ⅱ)设事件Ai表示“第i个月被投诉的次数为0”,
事件Bi表示“第i个月被投诉的次数为1”,
事件Ci表示“第i个月被投诉的次数为2”,
事件D表示“两个月内被投诉2次”
所以P(Ai)=0.3,P(Bi)=0.5,P(Ci)=0.2(i=1,2)
所以两个月中,一个月被投诉2次,另一个月被投诉0次的概率为P(A1C2+A2C1)
一、二月份均被投诉1次的概率为P(B1B2)
所以P(D)=P(A1C2+A2C1)+P(B1B2)=P(A1C2)+P(A2C1)+P(B1B2)
由事件的独立性的p(D)=0.3×0.2+0.2×0.3+0.5×0.5=0.37.
点评 本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案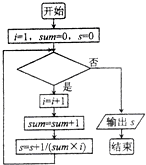
| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | 1 | B. | 13+$4\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{13}{2}+2\sqrt{3}$ |