题目内容
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.
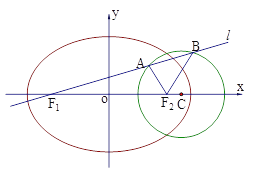
(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)
;(Ⅱ) ![]() 为定值,其值为2.
为定值,其值为2.
【解析】试题分析:(Ⅰ)通过计算圆心和半径得圆的方程,根据![]() 计算a的值,及焦点得c即可得椭圆方程;
计算a的值,及焦点得c即可得椭圆方程;
(Ⅱ)由直线和椭圆联立,利用韦达定理,利用坐标表示![]() ,计算即可定值.
,计算即可定值.
试题解析:
(Ⅰ)依题意知圆C的半径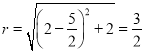 ,
,
∴圆C的标准方程为: ![]() ;
;
∵椭圆![]() 过点M
过点M![]() ,且焦点为
,且焦点为![]() 、
、![]() ,
,
由椭圆的定义得: ![]() ,
,
即![]() ,
,
∴![]() ,
, ![]() ,
,
∴椭圆E的方程为: ![]() .
.
【其它解法请参照给分】
(Ⅱ)显然直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,则
,则![]() 的方程为
的方程为![]() ,
,
由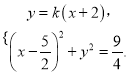 消去
消去![]() 得:
得:
![]() ,
,
显然![]() 有解,
有解,
设![]() 、
、![]() ,则
,则![]() ,
,
![]()
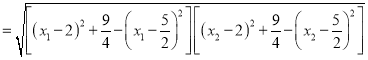
![]() .
.
故![]() 为定值,其值为2.
为定值,其值为2.

 字词句段篇系列答案
字词句段篇系列答案【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大。某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户按年龄分组进行访谈,统计结果如下表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [20,30) | 5 | 5 |
2 | [30.40) | 10 | 10 |
3 | [40.50) | 15 | 12 |
4 | [50.60) | 14 | 8 |
5 | [60,70) | 6 | 2 |
(1)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,则各组应分别抽取多少人?
(2)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(3)按以上统计数据填写下面2×2列联表,并判断以50岁为分界点,能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关;
年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | |||||
愿意使用的人数 | |||||||
不愿意使用的人数 | |||||||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

