题目内容
已知向量 ,函数
,函数 .
.
(1)求 的单调区间;
的单调区间;
(2)请说出 的图象是由
的图象是由 的图象经过怎样的变换得到的(说清每一步的变换方法);
的图象经过怎样的变换得到的(说清每一步的变换方法);
(3)当 时,求
时,求 的最大值及取得最大值时的
的最大值及取得最大值时的 的值。
的值。
(1)增区间: ;
;
减区间:
 ,此时
,此时
解析试题分析:(1)根据题意,由于向量 ,函数
,函数 =
= ,可知
,可知 为单调增区间,而减区间为
为单调增区间,而减区间为 ,
,
(2)由 先向左移动
先向左移动 个单位,然后将函数图像上的所有的点都缩短为原来的
个单位,然后将函数图像上的所有的点都缩短为原来的 ,再将函数图象整体向上平移一个单位得到,
,再将函数图象整体向上平移一个单位得到,
(3)同时当函数值取得最大值时,当 时,那么可知
时,那么可知 =
=  ,可知
,可知 ,那么可知函数取得最大值的变量的值为
,那么可知函数取得最大值的变量的值为
考点:三角函数的图像与性质
点评:解决的关键是利用向量的数量积公式化简表达式,借助于函数的性质来得到求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 b=
b= 。
。 及|a+ b|;
及|a+ b|;
 的最大值和最小值。
的最大值和最小值。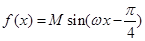 (
( )的部分图像如图所示.
)的部分图像如图所示.
 的解析式;
的解析式; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,且
,且 ,求角
,求角 中,内角
中,内角 所对的边长分别是
所对的边长分别是
 ,且
,且 的面积为
的面积为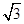 ,求
,求 的值;
的值; ,试判断
,试判断

 )+sin2x
)+sin2x ,cosB=
,cosB=
 求b.
求b. 的图像的一部分如图所示.
的图像的一部分如图所示.
 的解析式;
的解析式; 的最值;
的最值; .
.
 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图; 的图象作怎样的变换可得到
的图象作怎样的变换可得到 =(cos
=(cos x,sin
x,sin ,且x∈[0,
,且x∈[0, ].
].
 =
=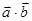 ,求函数
,求函数 的值。
的值。