题目内容
已知函数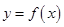 和
和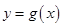 的图象关于
的图象关于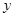 轴对称,且
轴对称,且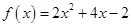 .
.
(1)求函数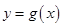 的解析式;
的解析式;
(2)当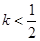 时,解不等式
时,解不等式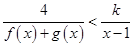 .
.
【答案】
(1)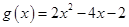 ;(2)当
;(2)当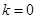 ,解集为
,解集为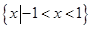 ;
;
当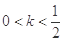 ,解集为
,解集为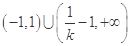 ;当
;当 ,解集为
,解集为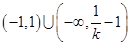 .
.
【解析】
试题分析:(1)先利用两个函数图象关于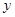 轴对称的关系,得出函数
轴对称的关系,得出函数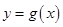 上的点
上的点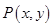 与其关于
与其关于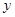 轴对称点
轴对称点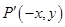 在函数
在函数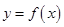 ,进而通过坐标之间的关系得出函数
,进而通过坐标之间的关系得出函数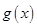 的解析式;(2)先将不的公式进行等价变形,得到
的解析式;(2)先将不的公式进行等价变形,得到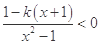 ,等价转化为
,等价转化为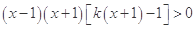 ,就
,就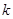 的取值进行分类讨论,主要是对
的取值进行分类讨论,主要是对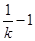 与
与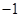 和
和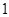 的大小进行分类讨论,从而确定不等式的解集.
的大小进行分类讨论,从而确定不等式的解集.
试题解析:(1)设函数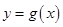 图象上任意一点
图象上任意一点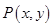 ,
,
由已知点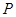 关于
关于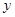 轴对称点
轴对称点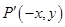 一定在函数
一定在函数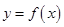 图象上,
图象上,
代入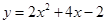 ,得
,得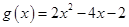 ;
;
(2)由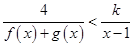 整理得不等式为
整理得不等式为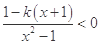 ,
,
等价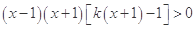 ,
,
当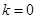 ,不等式为
,不等式为 ,解为
,解为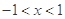 .
.
当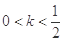 ,整理为
,整理为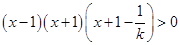 ,解为
,解为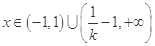 .
.
当 ,不等式整理为
,不等式整理为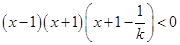 ,解为
,解为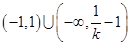 .
.
综上所述,当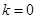 ,解集为
,解集为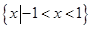 ;
;
当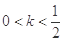 ,解集为
,解集为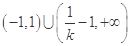 ;
;
当 ,解集为
,解集为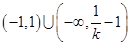 .
.
考点:1.函数图象的对称性;2.利用分类讨论法求解含参不等式

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
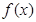 和
和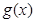 的图象关于原点对称,且
的图象关于原点对称,且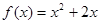 .
.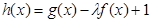 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数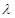 的取值范围
的取值范围 和
和 的图象关于原点对称,且
的图象关于原点对称,且 .
. ;
; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.