题目内容
正方体ABCD—EFGH的棱长为a,点P在AC上,Q在BG上,AP=BQ=a.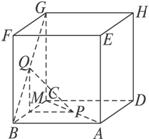
(1)求直线PQ与平面ABCD所成角的正切值;
(2)求证:PQ⊥AD.
(1)解析:作PM⊥BC于M,连结QM,
∵AB⊥BC,∴PM∥AB,于是![]() .∵AP=BQ,
.∵AP=BQ,
∴GQ=CP.这样可得![]() .
.
∴QM∥GC.
∵GC⊥平面AC,
∴QM⊥平面AC.
∠QPM是PQ与平面AC所成的角,
QM=![]() ,
,
∴tan∠QPM=![]() .
.
(2)证明:上面已证MP∥AB,QM∥GC,而AB⊥BC,QM⊥BC,
∴BC⊥MP,且BC⊥QM.
∴BC⊥平面PQM,因此BC⊥PQ.由AD∥BC可知PQ⊥AD.
小结:(1)中求直线PQ与平面ABCD所成角的正切值的过程是“作、证、算”,即先作出∠QPM,然后再证明∠QPM是PQ与平面ABCD所成角,最后再计算其正切值.(2)中证PQ⊥AD,由于BC∥AD,于是就把证PQ⊥AD的问题转化成了证明PQ⊥BC的问题.

练习册系列答案
相关题目
 8、如图,正方体ABCD-A1B1C1D1的棱长为2,动点E、F在棱A1B1上.点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P-EFQ的体积( )
8、如图,正方体ABCD-A1B1C1D1的棱长为2,动点E、F在棱A1B1上.点Q是CD的中点,动点P在棱AD上,若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P-EFQ的体积( )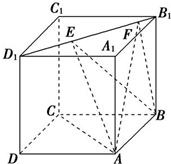 如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF= 如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为
如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为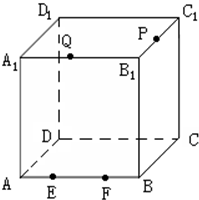 在棱长为a的正方体ABCD-A1B1C1D1中,P是C1B1的中点,若E,F都是AB上的点,且
在棱长为a的正方体ABCD-A1B1C1D1中,P是C1B1的中点,若E,F都是AB上的点,且 在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且
在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是D1D,BD的中点,G在棱CD上,且