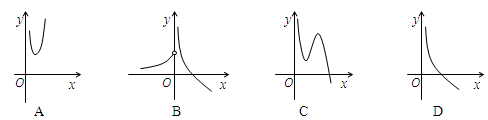题目内容
函数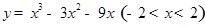 有( )
有( )
| A.极大值5,极小值 27 | B.极大值5,极小值 11 |
| C.极大值5,无极小值 | D.极小值 27,无极大值 |
C
解析试题分析:解:由已知得f′(x)=3x2-6x-9,f′(x)=0⇒x1=-1,x2=3,又函数f(x)的定义域是-2<x<2,则x变化时,f′(x)的变化情况如下:,当-2<x<-1时,f′(x)>0函数f(x)是增函数,当-1<x<2时,f′(x)<0函数f(x)是u减函数,所以当x=-1时,函数f(x)取得极大值为 5;无极小值,故答案为C
考点:导数的运用
点评:考查利用导数研究函数的极值问题,属基础题.

练习册系列答案
相关题目
若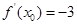 ,则
,则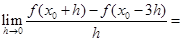 ( )
( )
A.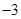 | B.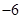 | C.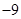 | D.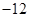 |
已知 是定义在
是定义在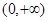 上的非负可导函数,且满足
上的非负可导函数,且满足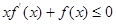 .对任意正数
.对任意正数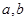 ,若
,若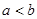 ,则必有( )
,则必有( )
A.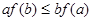 | B.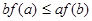 |
C.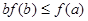 | D.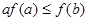 |
若 ,则
,则 等于( )
等于( )
A. | B. | C.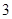 | D. |
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
已知曲线 在点
在点 处的切线经过点
处的切线经过点 ,则
,则 的值为
的值为
A. | B.1 | C.e | D.10 |
函数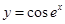 的导数是( )
的导数是( )
A.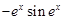 | B.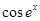 | C.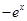 | D.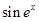 |
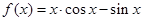 的导函数的部分图象为( )
的导函数的部分图象为( )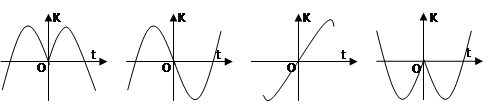
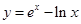 的图象是( )
的图象是( )