题目内容
设函数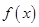 在定义域
在定义域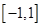 是奇函数,当
是奇函数,当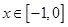 时,
时,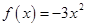 .
.
(1)当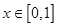 ,求
,求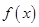 ;
;
(2)对任意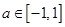 ,
,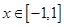 ,不等式
,不等式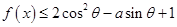 都成立,求
都成立,求 的取值范围.
的取值范围.
(1) 时,
时, ;(2)
;(2) .
.
解析试题分析:(1)设 ,可得
,可得 ,利用函数
,利用函数 为奇函数及当
为奇函数及当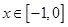 时,
时,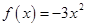 可得
可得 时,
时, ;(2)先将不等式
;(2)先将不等式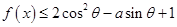 恒成立的问题转化为
恒成立的问题转化为 关于
关于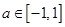 的不等式恒成立问题,注意此时
的不等式恒成立问题,注意此时 的最高次数为1或0,根据一次函数与常数函数的图像可得不等式组
的最高次数为1或0,根据一次函数与常数函数的图像可得不等式组 ,从中求解不等式组即可得出
,从中求解不等式组即可得出 的取值范围.
的取值范围.
试题解析:(1)依题意可知
设 ,则
,则 ,所以
,所以 6分
6分
(2)由(1)知 ,所以
,所以
 对
对 都成立
都成立 8分
8分
即 对
对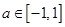 恒成立
恒成立
所以 10分
10分

所以 的取值范围为
的取值范围为 12分.
12分.
考点:1.函数的奇偶性;2.函数的解析式;3.函数的最值;4.不等式的恒成立问题.

练习册系列答案
相关题目
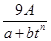 ,其中
,其中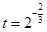 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 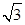 sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为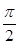 .
.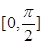 ,求点A的坐标.
,求点A的坐标. 的图象分别与
的图象分别与 轴相交于两点
轴相交于两点 ,且向量
,且向量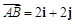 (
( 分别是与
分别是与 .
. 的值;
的值; 的解集为
的解集为 ,求
,求 的值
的值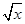 +2)=x+4
+2)=x+4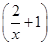 =lgx,求f(x);
=lgx,求f(x);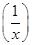 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x); 时,f
时,f >f
>f ;
; <0.
<0. a为常数且a∈(0,1).
a为常数且a∈(0,1). 时,求f
时,求f ;
;  ,
,