题目内容
已知抛物线C1：y2=2px(p＞0)的焦点F也是双曲线C2：
-
=1的一个焦点，过F作直线l与x轴垂直，l与C1交于A，B两点，l与C2交于C，D两点，则AB-CD=
| x2 |
| 4 |
| y2 |
| 5 |
7
7
．分析：先根据双曲线的标准方程，求得c，进而求得抛物线方程中的P，则抛物线方程可得，最后计算线段的长即可得出答案．
解答：
解：双曲线方程C2：
-
=1得：
a=2，b=
，c=3．
∴双曲线一个焦点坐标为F（3，0）
∴抛物线的焦点坐标为F（3，0）
∴p=6，
∴抛物线的方程为y2=12x，
∴CD=2CF=2×
=5，
AB=2AF=2
=12，
则AB-CD=7．
故答案为：7．
解：双曲线方程C2：| x2 |
| 4 |
| y2 |
| 5 |
a=2，b=
| 5 |
∴双曲线一个焦点坐标为F（3，0）
∴抛物线的焦点坐标为F（3，0）
∴p=6，
∴抛物线的方程为y2=12x，
∴CD=2CF=2×
| b2 |
| a |
AB=2AF=2
| 12×3 |
则AB-CD=7．
故答案为：7．
点评：本题主要考查了抛物线的简单性质，圆锥曲线的共同特征．考查了学生对基础知识的综合把握能力．
练习册系列答案
相关题目
（2012•河北模拟）已知抛物线C1：y2=2px和圆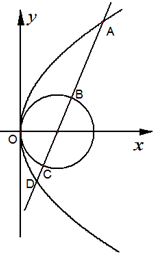
已知抛物线C1：y2=4x，圆C2：（x-1）2+y2=1，过抛物线焦点F的直线l交C1于A，D两点（点A在x轴上方），直线l交C2于B，C两点（点B在x轴上方）．