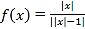题目内容
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]() ,(3)
,(3)![]()
【解析】
(1)根据对数单调性化简不等式,再解分式不等式得结果;
(2)先化简对数方程,再根据![]() 分类讨论方程根的情况,最后求得结果;
分类讨论方程根的情况,最后求得结果;
(3)先确定函数![]() 单调性,确定
单调性,确定![]() 最值取法,再化简不等式,根据二次函数单调性确定最值,解得结果.
最值取法,再化简不等式,根据二次函数单调性确定最值,解得结果.
(1)当![]() 时,
时,![]()
![]()
不等式解集为![]()
(2)![]()
![]()
①当![]() 时,
时,![]() 仅有一解
仅有一解![]() ,满足题意;
,满足题意;
②当![]() 时,则
时,则![]() ,
,
若![]() 时,解为
时,解为![]() ,满足题意;
,满足题意;
若![]() 时,解为
时,解为![]()
此时![]()
即有两个满足原方程的的根,所以不满足题意;
综上,![]() 或
或![]() ,
,
(3)因为![]() 在
在![]() 上单调递减,所以函数
上单调递减,所以函数![]() 在区间
在区间![]() 上的最大值与最小值的差为
上的最大值与最小值的差为![]() ,因此
,因此![]()
即![]() 对任意
对任意![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
因此![]()

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目