Question

设O为直角坐标系的原点,点M在定直线x=-p(p＞0)上移动,动点N在线段MO的延长线上且满足.

(1)求动点N的轨迹方程;

(2)说明点N的轨迹是什么曲线;

(3)当p=1时,求|MN|的最小值.

Answer 1

思路分析:本题考查轨迹问题及最值问题的解决方法.解题关键是利用点参数来求轨迹方程以及求最值时要注意掌握基本方法.

解:(1)设N(x,y)、M(-p,t),由M、O、N三点共线,得,即t=-.  ①

又由,得.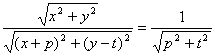

将①式代入化简,得.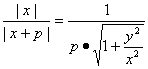

因为点N在线段MO的延长线上,所以x＞0.

又p＞0,所以上式化为x+p=p·.

化简,得(p²-1)x²+p²y²-2px-p²=0(p＞0),即为N点的轨迹方程.

(2)当p=1时,轨迹方程化为y²=2(x+)(x＞0),此时,轨迹是抛物线在y轴右侧的部分.

当p≠1时,轨迹方程为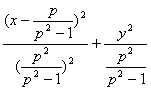=1(x＞0).

=1(x＞0).

∴当0＜p＜1时,此方程表示双曲线在y轴右侧的部分;

当p＞1时,方程表示椭圆在y轴右侧的部分.

(3)当p=1时,轨迹方程为y²=2x+1(x＞0),

设点N的坐标为(x,y),则点M的坐标为(-1,-).

因此|MN|=

=x++2≥2+2=4.