题目内容
选修4-4 坐标系与参数方程
已知两点A、B的极坐标分别为(4,
),(4,
).
(Ⅰ)求A、B两点间的距离;
(Ⅱ)以极坐标系的极点O为直角坐标系的原点,极轴为x轴的非负半轴,建立平面直角坐标系,求直线AB的参数方程.
已知两点A、B的极坐标分别为(4,
| π |
| 2 |
| π |
| 6 |
(Ⅰ)求A、B两点间的距离;
(Ⅱ)以极坐标系的极点O为直角坐标系的原点,极轴为x轴的非负半轴,建立平面直角坐标系,求直线AB的参数方程.
分析:(I)两点A、B的极坐标分别为(4,
),(4,
),化为直角坐标,再求A、B两点间的距离;
(II)根据A、B的直角坐标,求得直线AB的普通方程,可得直线的倾斜角,进而可求直线AB的参数方程.
| π |
| 2 |
| π |
| 6 |
(II)根据A、B的直角坐标,求得直线AB的普通方程,可得直线的倾斜角,进而可求直线AB的参数方程.
解答:解:(I)两点A、B的极坐标分别为(4,
),(4,
),化为直角坐标分别为A(0,4),B(2
,2)
∴A、B两点间的距离|AB|=
=4;
(II)∵A(0,4),B(2
,2)
∴直线AB的普通方程为
=
,即y=-
x+4,直线的倾斜角为150°
∴直线AB的参数方程为
(t为参数)
| π |
| 2 |
| π |
| 6 |
| 3 |
∴A、B两点间的距离|AB|=
| 12+4 |
(II)∵A(0,4),B(2
| 3 |
∴直线AB的普通方程为
| y-4 |
| 2-4 |
| x-0 | ||
2
|
| ||
| 3 |
∴直线AB的参数方程为
|
点评:本题考查极坐标与直角坐标的互化,考查直线的参数方法,掌握互化方法是关键.

练习册系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题) .以极点为平面直角坐标系的原点,极轴为x
.以极点为平面直角坐标系的原点,极轴为x 的参数方程是
的参数方程是 ,
, (2)(选修4—5 不等式选讲)已知
(2)(选修4—5 不等式选讲)已知 ,且
,且  ,则
,则 的最小值为 .
的最小值为 . ,
, ,
,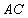 与
与 交于点D,
交于点D, ,
, ,则
,则 .
.