题目内容
现有一个关于平面图形的命题:如图所示,同一个平面内有两个变长都是a的正方形,其中一个正方形的某起点在另一个正方形的中心,则这两个正方形重叠部分的面积恒为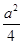 ,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___
,类比到空间,有两个棱长为a的正方体,其中某一个正方体的某顶点在另一个正方体的中心,则这两个正方体的重叠部分的体积恒为___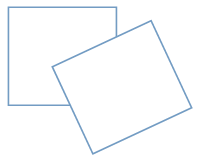

解析试题分析:解:同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,
则这两个正方形重叠部分的面积恒为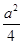
类比到空间有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,
则这两个正方体重叠部分的体积恒为 ,
,
故答案为 .
.
考点:类比推理.
点评:本题主要考查类比推理的知识点,解答本题的关键是根据平面中正方形的性质类比推理出空间正方体的性质特征,本题难度不是很大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在如下数表中,已知每行、每列中的数都成等差数列,
| | 第1列 | 第2列 | 第3列 | … |
| 第1行 | 1 | 2 | 3 | … |
| 第2行 | 2 | 4 | 6 | … |
| 第3行 | 3 | 6 | 9 | … |
| … | … | … | … | … |
 (n∈N*),经计算得f(4)>2,f(8)>
(n∈N*),经计算得f(4)>2,f(8)> ,f(16)>3,f(32)>
,f(16)>3,f(32)> ,……,观察上述结果,则可归纳出一般结论为 。
,……,观察上述结果,则可归纳出一般结论为 。 的项是由1或2构成,且首项为1,在第
的项是由1或2构成,且首项为1,在第 个1和第
个1和第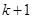 个1之间有
个1之间有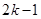 个2,即数列
个2,即数列 项和为
项和为 ,则
,则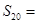 ;
;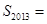 .
. 的解”有如下解题思路:设
的解”有如下解题思路:设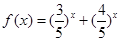 ,则
,则 在
在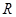 上单调递减,且
上单调递减,且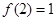 ,所以原方程有唯一解
,所以原方程有唯一解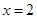 .类比上述解题思路,方程
.类比上述解题思路,方程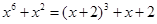 的解集为 .
的解集为 . 作曲线
作曲线 :
: 的切线,切点为
的切线,切点为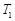 ,设
,设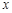 轴上的投影是点
轴上的投影是点 ,过点
,过点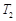 ,设
,设 ,…,依次下去,得到第
,…,依次下去,得到第
 个切点
个切点 .则点
.则点 的
的 次方幂有如下分解方式:
次方幂有如下分解方式:







 的分解中最小的数是73,则
的分解中最小的数是73,则 的三边长为
的三边长为 ,内切圆半径为
,内切圆半径为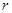 (用
(用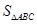 表示
表示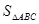
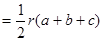 ;类比这一结论有:若三棱锥
;类比这一结论有:若三棱锥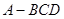 的内切球半径为
的内切球半径为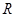 ,则三棱锥体积
,则三棱锥体积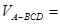 ___________________________.
___________________________.