题目内容
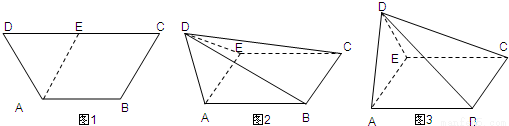
如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.(1)当平面ADE折到与底面ABCE所成的二面角为90时,如图3所示,求此时二面角A-BD-C平面角的余弦值.
(2)在将△ADE开始折起到与△ABE重合的过程中,求直线DC与平面ABCE所成角的正切值的取值范围.
【答案】分析:(1)在图3中取AE中点O,可取O为原点建立直角坐标系,分别求出平面ABD法向量与平面CBD的法向量,最后利用向量的夹角公式求出夹角的余弦值,即为二面角平面角的余弦值;
(2)在折动过程中,直线DC与平面ABCE所成的角为∠DCF,设DF=t∈ ,则
,则 ,设g(t)=
,设g(t)= ,
, ,然后利用导数研究函数g(x)的最值即可求出所求.
,然后利用导数研究函数g(x)的最值即可求出所求.
解答:
解:(1)在图3中取AE中点O,建立直角坐标系.
∵平面DAE⊥平面ABCE,DO⊥AE,DO?平面DAE,平面DAE∩平面ABCE=AE
∴DO⊥平面ABCE
易知BA=BE∴BO⊥AC∴可取O为原点建立直角坐标系(2分)

设平面ABD法向量为 ,平面CBD法向量为
,平面CBD法向量为
则 ⇒
⇒
∴可取平面ABD法向量

∴可取平面ABD法向量
 (7分)
(7分)
(2)在图2中作DF⊥D′B,交D′B于F点.易证DO⊥AE,D'O⊥AE,
∴AE⊥平面DD′B∴AE⊥DF又DF⊥DB,∴DF⊥面ABCE.
∴在折动过程中,直线DC与平面ABCE所成的角为∠DCF,
设DF=t∈ ,则
,则 .
.
 ,
,
∴ ,
,
设g(t)= ,
, ,则
,则 ,
,
 时,
时,
∴ 时,
时, ,
,
即 时,tan∠DCF最大值为
时,tan∠DCF最大值为 .
.
点评:本题主要考查了利用空间向量度量二面角的平面角以及线面所成角,同时考查了空间想象能力和计算能力,属于中档题.
(2)在折动过程中,直线DC与平面ABCE所成的角为∠DCF,设DF=t∈
 ,则
,则 ,设g(t)=
,设g(t)= ,
, ,然后利用导数研究函数g(x)的最值即可求出所求.
,然后利用导数研究函数g(x)的最值即可求出所求.解答:

解:(1)在图3中取AE中点O,建立直角坐标系.
∵平面DAE⊥平面ABCE,DO⊥AE,DO?平面DAE,平面DAE∩平面ABCE=AE
∴DO⊥平面ABCE
易知BA=BE∴BO⊥AC∴可取O为原点建立直角坐标系(2分)

设平面ABD法向量为
 ,平面CBD法向量为
,平面CBD法向量为
则
 ⇒
⇒
∴可取平面ABD法向量


∴可取平面ABD法向量

 (7分)
(7分)(2)在图2中作DF⊥D′B,交D′B于F点.易证DO⊥AE,D'O⊥AE,
∴AE⊥平面DD′B∴AE⊥DF又DF⊥DB,∴DF⊥面ABCE.
∴在折动过程中,直线DC与平面ABCE所成的角为∠DCF,
设DF=t∈
 ,则
,则 .
. ,
,∴
 ,
,设g(t)=
 ,
, ,则
,则 ,
, 时,
时,
∴
 时,
时, ,
,即
 时,tan∠DCF最大值为
时,tan∠DCF最大值为 .
.点评:本题主要考查了利用空间向量度量二面角的平面角以及线面所成角,同时考查了空间想象能力和计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
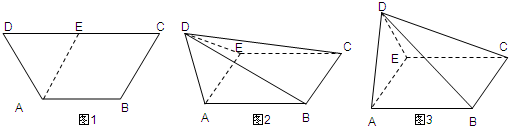 如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示.
如图1,等腰梯形ABCD中,AB=2,CD=4,∠ADC=∠BCD=60°.取线段CD中点E,将△ADE沿AE折起,如图2所示. 如图1,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.将△ABE沿AE折起后如图2,使二面角B-AE-C成直二面角,设F是CD的中点,P是棱BC的中点.
如图1,等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.将△ABE沿AE折起后如图2,使二面角B-AE-C成直二面角,设F是CD的中点,P是棱BC的中点.

