Question

已知矩形ABCD，AD=2AB=2，点E是AD的中点，将△DEC沿CE折起到△D’EC的位置，使二面角D'-EC -B是直二面角。

(Ⅰ) 证明：BE⊥CD’；

(Ⅱ) 求二面角D'-BC -E的余弦值，

Answer 1

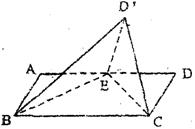
解：(Ⅰ)∵AD=2AB=2，E是AD的中点，

    ∴△BAE，△CDE是等腰直角三角形，∠BEC=90°，即

    又∵平面D'EC⊥平面BEC，面D'EC∩面BEC=EC

     ∴BE⊥面D'EC，∴BE⊥CD’．               ……………4分

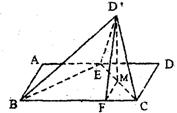
    (Ⅱ)法一：设M是线段EC的中点，过M作MF⊥BC

    垂足为F，连接D’M，D'F,则D'M⊥EC.

    ∵平面D'EC⊥平面BEC  ∴D'M⊥平面EBC

∴MF是D'F在平面BEC上的射影，由三垂线定理得：D'F⊥BC

∴∠D'FM是二面D'-BC-E的平面角．…………8分

在Rt△D'MF中，,

,

∴二面角D’-BC—E的余弦值为  …………………………………………………14分，

法二：如图，以EB，EC为x轴、y轴，过E垂直于平面BEC的射线为z轴，建立空间直角坐标系．

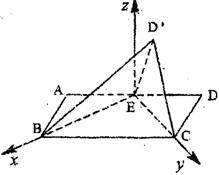
则             ……………8分

设平面BEC的法向量为；平面D'BC的法向量为

,

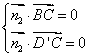
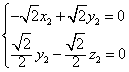     取x₂=l………12分

得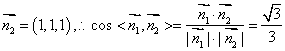

∴二面角D'-BC-E的余弦值为………………14分[来源:Z.xx.k.C