题目内容
3.已知函数f(x)=$\frac{{x}^{2}}{ax+b}$(a,b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.(1)求函数f(x)的解析式
(2)若$\frac{1}{f(x)}$+k-1>0恒成立,求k的范围.
分析 (1)由f(x)解析式得方程,把方程的解代入得关于a,b的方程组,求出a,b即可.
(2)$\frac{1}{f(x)}$+k-1>0恒成立,则k>1+$\frac{x-2}{{x}^{2}}$,求出右边的最大值,即可求k的范围.
解答 解:(1)依已知条件可知方程f(x)-x+12=0即为$\frac{{x}^{2}}{ax+b}$-x+12=0
∵x1=3,x2=4是上述方程的解,
∴$\left\{\begin{array}{l}{\frac{9}{3a+b}-3+12=0}\\{\frac{16}{a+b}-4+12=0}\end{array}\right.$,解得a=-1,b=2,
则函数的解析式为f(x)=-$\frac{{x}^{2}}{x-2}$;
(2)$\frac{1}{f(x)}$+k-1>0恒成立,则k>1+$\frac{x-2}{{x}^{2}}$,
∵1+$\frac{x-2}{{x}^{2}}$=-2($\frac{1}{x}$-$\frac{1}{4}$)2+$\frac{9}{8}$≤$\frac{9}{8}$,
∴k>$\frac{9}{8}$.
点评 用待定系数法求函数解析式是一种常用的重要的方法,是基本技能,分离参数求最值是解决恒成立问题的常用方法.

练习册系列答案
相关题目
13.在△ABC中,tan$\frac{A+B}{2}$=2sinC,若AB=1,则△ABC的周长为( )
| A. | 1+2sin(A+$\frac{π}{6}$) | B. | 1+2sin(A+$\frac{π}{3}$) | C. | 1+sin(A+$\frac{π}{6}$) | D. | 1+sin(A+$\frac{π}{3}$) |
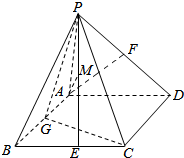 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点