题目内容
已知 ,
, 是不共线的向量,且
是不共线的向量,且 =λ1
=λ1 +
+ ,
, =
= +λ2
+λ2 ,(λ1,λ2∈R),若A、B、C三点共线,则λ1,λ2满足( )
,(λ1,λ2∈R),若A、B、C三点共线,则λ1,λ2满足( )A.λ1=λ2=-1
B.λ1=λ2=1
C.λ1λ2-1=0
D.λ1λ2+1=0
【答案】分析:根据两个向量共线的充要条件,必存在非零实数k,使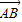 =k
=k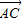 ,结合题中
,结合题中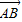 、
、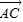 关于
关于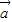 、
、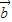 的式子,化简即可得到正确答案.
的式子,化简即可得到正确答案.
解答:解:∵A、B、C三点共线,
∴存在非零实数k,使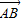 =k
=k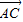
∵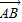 =λ1
=λ1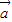 +
+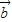 ,
,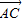 =
=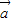 +λ2
+λ2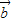 ,
,
∴λ1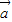 +
+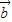 =k(
=k(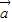 +λ2
+λ2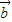 ),得λ1=k且1=kλ2,
),得λ1=k且1=kλ2,
两式消去k,得λ1λ2=1,即λ1λ2-1=0
故选C
点评:本题给出两个向量共线,求参数满足的相等关系,着重考查了向量共线的充要条件和平面向量基本定理等知识,属于基础题.
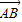 =k
=k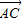 ,结合题中
,结合题中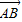 、
、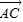 关于
关于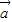 、
、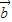 的式子,化简即可得到正确答案.
的式子,化简即可得到正确答案.解答:解:∵A、B、C三点共线,
∴存在非零实数k,使
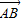 =k
=k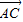
∵
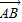 =λ1
=λ1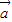 +
+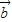 ,
,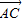 =
=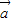 +λ2
+λ2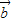 ,
,∴λ1
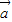 +
+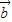 =k(
=k(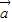 +λ2
+λ2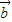 ),得λ1=k且1=kλ2,
),得λ1=k且1=kλ2,两式消去k,得λ1λ2=1,即λ1λ2-1=0
故选C
点评:本题给出两个向量共线,求参数满足的相等关系,着重考查了向量共线的充要条件和平面向量基本定理等知识,属于基础题.

练习册系列答案
相关题目
 、
、 是不共线的向量,
是不共线的向量, ,
,
 ,则
,则 、
、 、
、 三点共线的充要条件是
三点共线的充要条件是 B.
B.
 C.
C.
 D.
D.

 、
、 是不共线的向量,
是不共线的向量, =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),那么A、B、C三点共线的充要条件为( )
(λ,μ∈R),那么A、B、C三点共线的充要条件为( ) 、
、 是不共线的向量,
是不共线的向量, =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),那么A、B、C三点共线的充要条件为( )
(λ,μ∈R),那么A、B、C三点共线的充要条件为( ) 、
、 是不共线的向量,
是不共线的向量, =λ
=λ +
+ ,
, =
= +μ
+μ (λ,μ∈R),那么A、B、C三点共线的充要条件为( )
(λ,μ∈R),那么A、B、C三点共线的充要条件为( )