题目内容
5. 如图,在多面体ABCDE中,CD和BE都垂直于平面ABC,且∠ACB=90°,AB=4,BE=1,CD=3,DE=2$\sqrt{2}$.
如图,在多面体ABCDE中,CD和BE都垂直于平面ABC,且∠ACB=90°,AB=4,BE=1,CD=3,DE=2$\sqrt{2}$.(Ⅰ)求证:BE∥平面ACD;
(Ⅱ)求多面体ABCDE的体积.
分析 (Ⅰ)证明BE∥CD,利用线面平行的判定即可证明BE∥平面ACD;
(Ⅱ)在平面BCDE内过点E作EF∥BC,交CD于点F,证明四边形BCDE是直角梯形,AC⊥平面DCBE,即可求多面体ABCDE的体积.
解答 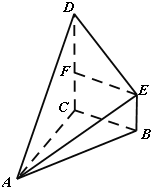 (Ⅰ)证明:因为CD和BE都垂直于平面ABC,所以BE∥CD,
(Ⅰ)证明:因为CD和BE都垂直于平面ABC,所以BE∥CD,
又CD?平面ACD,BE?平面ACD,
所以BE∥平面ACD. …(5分)
(Ⅱ)解:因为CD和BE都垂直于平面ABC,所以BE∥CD,
则四边形BCDE是直角梯形,…(6分)
在平面BCDE内过点E作EF∥BC,交CD于点F,
因为BE=1,CD=3,DE=2$\sqrt{2}$,…(7分)
在直角三角形DEF中,EF=2,
所以BC=EF=2,…(8分)
在直角三角形ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$,…(9分)
因为AC⊥BC,AC⊥DC,所以AC⊥平面DCBE,
而四边形BCDE的面积S=$\frac{1}{2}$(BE+CD)•BC=4,…(10分)
因此多面体ABCDE的体积为V=$\frac{1}{3}S•AC$=$\frac{8}{3}\sqrt{3}$. …(12分)
点评 本题考查空间直线与平面之间的位置关系,线面平行,体积等知识,高考必考内容,考查空间想象能力和逻辑思维推理能力.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
16.已知函数f(x)=log2(1+x)-log2(1-x),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数也是偶函数 | D. | 既不是奇函数也不是偶函数 |
20.如图是某几何体的三视图,且正视图与侧视图相同,则这个几何体的表面积是( )


| A. | $\frac{4}{3}$π | B. | 7π | C. | (5+$\sqrt{5}$)π | D. | (4+$\sqrt{5}$)π |
10.在五张卡片上分别写出有2,3,4,5,6这5个数字,其中6可以当9使用,从中任取3张,组成三位数,这样的三位数个数为( )
| A. | 60个 | B. | 70个 | C. | 96个 | D. | 136个 |
17.已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若m∥n,m∥α,则n∥α | ||
| C. | 若α∩β=n,m∥α,m∥β,则m∥n | D. | 若m⊥α,m⊥n,则n∥α |