题目内容
已知椭圆C:![]() (a>b>0).F1,F2分别为椭圆C的左,右焦点,A1,A2分别为椭圆C的左,右顶点.过右焦点F2且垂直于x轴的直线与椭圆C在第一象限的交点为M(
(a>b>0).F1,F2分别为椭圆C的左,右焦点,A1,A2分别为椭圆C的左,右顶点.过右焦点F2且垂直于x轴的直线与椭圆C在第一象限的交点为M(![]() ,2).
,2).

(1)求椭圆C的标准方程;
(2)直线l:x=my+1与椭圆C交于P,Q两点,直线A1P与A2Q交于点S.当直线l变化时,点S是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
答案:
解析:
解析:
|
解:(1) (2)当 当 若定直线存在,则方程应是 下面给予证明. 把 当 须 而 综上,定直线方程为 (其它解法酌情给分) |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
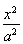









 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3. (a>b>0)的离心率为
(a>b>0)的离心率为 短轴一个端点到右焦点的
短轴一个端点到右焦点的 .
. ,求△AOB面积的
,求△AOB面积的