题目内容
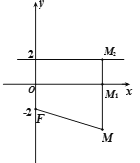
【题目】已知四边形![]() ,点
,点![]() 为线段
为线段![]() 的中点,且
的中点,且![]()
![]() .
. ![]() ,
, ![]() .现将△
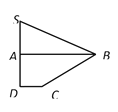
.现将△![]() 沿
沿![]() 进行翻折,使得
进行翻折,使得![]()
![]() °,得到图形如图所示,连接
°,得到图形如图所示,连接![]() .
.
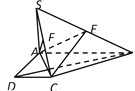
(Ⅰ)若点![]() 在线段
在线段![]() 上,证明:
上,证明: ![]() ;
;
(Ⅱ)若![]() 点为
点为![]() 的中点,求点
的中点,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)根据线面垂直判定与性质定理得![]() ,再根据平几知识计算得
,再根据平几知识计算得![]() ,最后根据线面垂直判定与性质定理得结论,(Ⅱ)根据等体积法求点
,最后根据线面垂直判定与性质定理得结论,(Ⅱ)根据等体积法求点![]() 到平面
到平面![]() 的距离.
的距离.
(Ⅰ)证明:在图中,因为![]()
![]() °,则
°,则![]() ,
,
又![]() ,
,![]() ,故
,故![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ;
;
在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
,
又![]() °,所以
°,所以![]() °,即
°,即![]() ;又
;又![]() ,故
,故![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,故
,故![]() .
.
(Ⅱ)设点![]() 到平面
到平面![]() 的距离
的距离![]() ,因为
,因为![]() ,
,
即![]() 其中
其中![]() ,
,![]() ,
,
在△AEC中,![]() ,
,![]() ,
,
取AB中点G,连接EG,CG,易证EG∥SA,从而EG⊥平面ABCD,EG⊥CG,
所以![]() ,
,![]()
故 ,即点
,即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目