题目内容
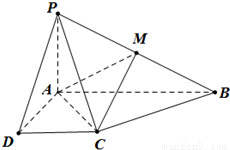
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:(1)PA∥平面BDE;
(2)平面PAC⊥平面PBD.

【答案】分析:(1)利用线面平行的判定定理判定.(2)利用面面垂直的判定定理判定.
解答: 解:证明:(1)连结AC交BD于点O,连结OE.
解:证明:(1)连结AC交BD于点O,连结OE.
∵四边形ABCD是菱形,∴AO=CO.
∵E为PC的中点,∴EO∥PA.
∵PA?平面BDE,EO?平面BDE,
∴PA∥平面BDE.
(2)∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵四边形ABCD是菱形,
∴BD⊥AC.∵AC∩PA=A,
∴BD⊥平面PAC,
∵BD?平面PBD,
∴平面PAC⊥平面PBD.
点评:本题主要考查线面平行和面面垂直的判定,要求熟练掌握相关的判定定理.
解答:
 解:证明:(1)连结AC交BD于点O,连结OE.
解:证明:(1)连结AC交BD于点O,连结OE.∵四边形ABCD是菱形,∴AO=CO.
∵E为PC的中点,∴EO∥PA.
∵PA?平面BDE,EO?平面BDE,
∴PA∥平面BDE.
(2)∵PA⊥平面ABCD,BD?平面ABCD,
∴PA⊥BD,
∵四边形ABCD是菱形,
∴BD⊥AC.∵AC∩PA=A,
∴BD⊥平面PAC,
∵BD?平面PBD,
∴平面PAC⊥平面PBD.
点评:本题主要考查线面平行和面面垂直的判定,要求熟练掌握相关的判定定理.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:
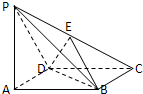
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证: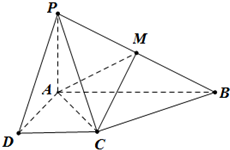 在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点. (2013•河池模拟)在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
(2013•河池模拟)在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.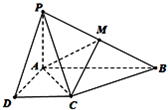 在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.