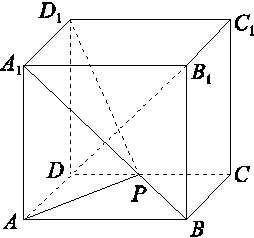
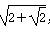题目内容
定义运算:xy=
例如:34=3,(-2)4=4,则函数f(x)=x2(2x-x2)的最大值为________.
4
[解析] 依题意得,当x2(2x-x2)≥0,即0≤x≤2时,f(x)=x2的最大值是22=4;当x2(2x-x2)<0,即x<0或x>2时,f(x)=2x-x2=-(x-1)2+1<0.因此,函数f(x)的最大值是4.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
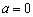 是复数
是复数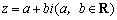 为纯虚数的( )
为纯虚数的( ) ≤0的解集为( )
≤0的解集为( )
 所表示的平面区域为D.在映射T:
所表示的平面区域为D.在映射T: 的作用下,区域D内的点(x,y)对应的象为点(u,v),则由点(u,v)所形成的平面区域的面积为( )
的作用下,区域D内的点(x,y)对应的象为点(u,v),则由点(u,v)所形成的平面区域的面积为( )