题目内容
已知函数f（x）=x（x-a）（x-b），其中a、b∈R（I）当a=0，b=3时，求函数，f（x）的极值；
（Ⅱ）当a=0时，
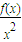-lnx≥0在[1，+∞）上恒成立，求b的取值范围（Ⅲ）若0＜a＜b，点A（s，f（s）），B（t，f（t））分别是函数f（x）的两个极值点，且0A⊥OB，其中0为原点，求a+b的取值范围．
【答案】分析：（I）求导数，确定函数的单调性，即可求函数的极值；
（Ⅱ）当a=0时，
-lnx=x-b-lnx≥0在[1，+∞）上恒成立，即b≤x-lnx在[1，+∞）上恒成立，求出右边的最小值，即可得到结论；
（Ⅲ）利用向量知识，确定
，进而可得
，利用基本不等式，即可得到结论．
解答：解：（I）当a=0，b=3时，f（x）=x3-3x2
∴f′（x）=3x2-6x=3x（x-2）
令f′（x）＞0，可得x＜0或x＞2，令f′（x）＜0，可得0＜x＜2
∴x=0时，函数取得极大值为0，x=2时，函数取得极小值为-4；
（Ⅱ）当a=0时，
-lnx=x-b-lnx≥0在[1，+∞）上恒成立，
∴b≤x-lnx在[1，+∞）上恒成立
令g（x）=x-lnx，则
∵x＞1，∴
∴g（x）在[1，+∞）上是增函数
∴g（x）min=g（1）=1
∴b≤1；
（Ⅲ）由题意，
，∴st+f（s）f（t）=0
∴st+st（s-a）（s-b）（t-a）（t-b）=0①
∴f′（x）=3x2-2（a+b）x+ab
∵s，t是f′（x）=0的两根
∴s+t=
，st=
＞0
∴①可化为（
）（
）=-1
∴ab（a-b）2=9
∴
∴
∴
≥12
当且仅当
，即ab=
时取“=”
∴a+b的取值范围是[2
，+∞）．
点评：本题考查导数知识的运用，考查函数的单调性与极值，考查函数的最值，考查学生分析解决问题的能力，属于中档题．
（Ⅱ）当a=0时，
-lnx=x-b-lnx≥0在[1，+∞）上恒成立，即b≤x-lnx在[1，+∞）上恒成立，求出右边的最小值，即可得到结论；（Ⅲ）利用向量知识，确定
，进而可得，利用基本不等式，即可得到结论．解答：解：（I）当a=0，b=3时，f（x）=x3-3x2
∴f′（x）=3x2-6x=3x（x-2）
令f′（x）＞0，可得x＜0或x＞2，令f′（x）＜0，可得0＜x＜2
∴x=0时，函数取得极大值为0，x=2时，函数取得极小值为-4；
（Ⅱ）当a=0时，
-lnx=x-b-lnx≥0在[1，+∞）上恒成立，∴b≤x-lnx在[1，+∞）上恒成立
令g（x）=x-lnx，则
∵x＞1，∴
∴g（x）在[1，+∞）上是增函数
∴g（x）min=g（1）=1
∴b≤1；
（Ⅲ）由题意，
，∴st+f（s）f（t）=0∴st+st（s-a）（s-b）（t-a）（t-b）=0①
∴f′（x）=3x2-2（a+b）x+ab
∵s，t是f′（x）=0的两根
∴s+t=
，st=＞0∴①可化为（
）（）=-1∴ab（a-b）2=9
∴
∴
∴
≥12当且仅当
，即ab=时取“=”∴a+b的取值范围是[2
，+∞）．点评：本题考查导数知识的运用，考查函数的单调性与极值，考查函数的最值，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|