题目内容
(12分)设函数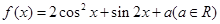
(1)求函数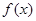 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当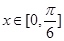 时,
时,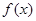 的最大值为2,求
的最大值为2,求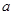 的值,并求出
的值,并求出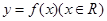 的对称
的对称
轴方程.
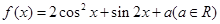
(1)求函数
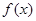 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(2)当
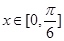 时,
时,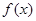 的最大值为2,求
的最大值为2,求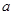 的值,并求出
的值,并求出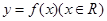 的对称
的对称轴方程.
解:(1)

则
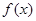 的最小正周期
的最小正周期 , ……………………………4分
, ……………………………4分且当
 时
时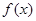 单调递增.
单调递增.即
 为
为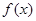 的单调递增区间(写成开区间不
的单调递增区间(写成开区间不扣分).…………6分
(2)当
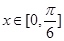 时
时 ,
,当
 ,即
,即 时
时 .
.所以
 . ……………9分
. ……………9分 为
为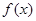 的对称轴. ……12分
的对称轴. ……12分略

练习册系列答案
相关题目
 ,函数
,函数 的最大值为
的最大值为 ,则实数
,则实数 的值为 .
的值为 .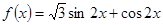 ,下面结论错误的是
,下面结论错误的是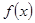 的最小正常周期为
的最小正常周期为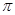
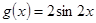 向左平移
向左平移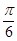 个单位得到
个单位得到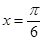 对称
对称 ,
, ,
, ,其中
,其中 .
.  时,求
时,求 值的集合;
值的集合;  的最大值.
的最大值.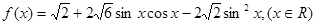
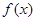 的图像作如下变换:先将
的图像作如下变换:先将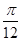 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数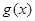 的图像,求
的图像,求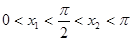 ,且
,且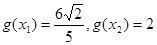 ,求
,求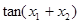 的值。
的值。 .
. 的单调区间;
的单调区间; 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间 上的最小值和最大值.
上的最小值和最大值. (其中
(其中 )的最大值为2,直线
)的最大值为2,直线 是
是 的图象的任意两条对称轴,且
的图象的任意两条对称轴,且 的最小值为
的最小值为
 的值;
的值; 的值。
的值。 且满足
且满足
 的单调递增区间;
的单调递增区间; 的内角A满足
的内角A满足 且
且 ,求边BC的最小值.
,求边BC的最小值. ,则
,则 的值为
的值为


