题目内容

19．在三棱锥A-BCD中，侧棱AB，AC，AD两两垂直，△ABC，△ACD，△ADB的面积分别为10，5，4，则该三棱锥外接球的表面积为（　　）
A．141πB．45πC．3$\sqrt{5}$πD．24π

分析 三棱锥A-BCD中，侧棱AB、AC、AD两两垂直，补成长方体，两者的外接球是同一个，长方体的对角线就是球的直径，求出长方体的三度，转化为对角线长，即可求解外接球的表面积．

解答 解：三棱锥A-BCD中，侧棱AB、AC、AD两两垂直，补成长方体，两者的外接球是同一个，长方体的对角线就是球的直径，
设长方体的三度为a，b，c由题意得：ab=20，ac=10，bc=8，
解得：a=5，b=4，c=2，
所以球的直径为：$\sqrt{25+16+4}$=3$\sqrt{5}$，
它的半径为$\frac{3\sqrt{5}}{2}$，
球的表面积为$4π•（\frac{3\sqrt{5}}{2}）^{2}$=45π，
故选：B．

点评 本题是基础题，考查几何体的外接球的体积，三棱锥转化为长方体，两者的外接球是同一个，以及长方体的对角线就是球的直径是解题的关键所在．

练习册系列答案
相关题目
3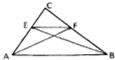．如图直角三角形ABC中，|CA|=|CB|，|AB|=3，点E、F分别在CA、CB上，且EF∥AB，AE=$\sqrt{2}$，则$\overrightarrow{AF}$•$\overrightarrow{BE}$=（　　）
A．3B．-3C．0D．-7
10．在△ABC中，内角A、B、C的对边分别是a、b、c，若a2+b2=4a+2b-5，且a2=b2+c2-bc，则S△ABC=$\frac{{\sqrt{39}+\sqrt{3}}}{8}$．
7．若直线2x+y-2$\sqrt{5}$=0过双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个焦点，且与双曲线的一条渐近线垂直，则双曲线的方程为（　　）
A．$\frac{{x}^{2}}{4}-{y}^{2}=1$B．x2-$\frac{{y}^{2}}{4}=1$C．$\frac{{x}^{2}}{10}-\frac{{y}^{2}}{5}=1$D．$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{4}=1$
14．设集合S={x|x＞-3}，T={x|-6≤x≤1}，则S∪T=（　　）
A．[-6，+∞）B．（-3，+∞）C．[-6，1]D．（-3，1]
4．学校开展阳光体育活动，对学生的锻练时间进行随机抽样调查，从中随机抽取男、女生各25名进行了问卷调查，得到了如下列联表：
锻练时间男生女生合计
少于1小时51520
不少于1小时201030
合  计252550
（Ⅰ） 根据上表数据求x，y，并据此资料分析：有多大的把握可以认为“锻练时间与性别有关”？
（Ⅱ） 从这50名学生中用分层抽样的方法抽取5人为样本，求从该样本中任取2人，
至少有1人锻练时间少于1小时的概率．
K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
P（K2≥K0）0.050.0250.0100.0050.001
k03.8415.0246.6357.87910.828
11．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1，F2，过点F1作直线l⊥x轴交双曲线C的渐近线于点A，B若以AB为直径的圆恰过点F2，则该双曲线的离心率为（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．2D．$\sqrt{5}$
8．已知函数f（x）=1-$\frac{a}{x}+ln\frac{1}{x}$（a为实数）．
（Ⅰ）当a=1时，求函数f（x）的图象在点$（\frac{1}{2}，f（\frac{1}{2}））$处的切线方程；
（Ⅱ）设函数h（a）=3λa-2a2（其中λ为常数），若函数f（x）在区间（0，2）上不存在极值，且存在a满足h（a）≥λ+$\frac{1}{8}$，求λ的取值范围；
（Ⅲ）已知n∈N*，求证：ln（n+1）＜1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+…+\frac{1}{n}$．
9．若复数z满足z•（2-i）=1（i为虚数单位），则|z|=（　　）
A．$\frac{{\sqrt{5}}}{3}$B．$\frac{1}{5}$C．$\sqrt{5}$D．$\frac{{\sqrt{5}}}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网