题目内容
在数列{an}中,已知a1=-2,an+1=- ,n∈N*。
,n∈N*。
(1)设bn= ,n∈N*,求数列{bn}的通项公式;
,n∈N*,求数列{bn}的通项公式;
(2)设{bn}的前n项和为Sn,若不等式Sn-kbn<k对任意n∈N*恒成立,求k的取值范围。
 ,n∈N*。
,n∈N*。(1)设bn=
 ,n∈N*,求数列{bn}的通项公式;
,n∈N*,求数列{bn}的通项公式;(2)设{bn}的前n项和为Sn,若不等式Sn-kbn<k对任意n∈N*恒成立,求k的取值范围。
解:(1)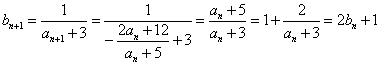
进而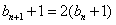
于是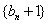 是以
是以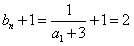 为首项,2为公比的等比数列
为首项,2为公比的等比数列
故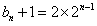 ,
,
即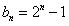 。
。
(2)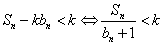
而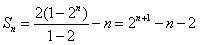
∴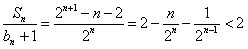
∴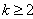 。
。
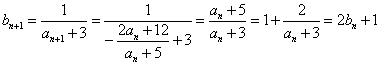
进而
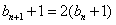
于是
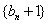 是以
是以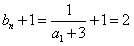 为首项,2为公比的等比数列
为首项,2为公比的等比数列故
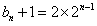 ,
,即
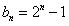 。
。(2)
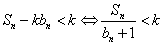
而
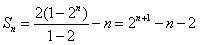
∴
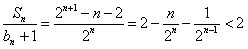
∴
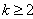 。
。
练习册系列答案
相关题目