题目内容
对于数列{λn},若存在常数M>0,对任意n∈N+,恒有|λn+1-λn|+|λn-λn-1|+…+|λ2-λ1|≤M,则称数列{λn}为∂-数列.
求证:
(1)设Sn是数列{an}的前n项和,若{Sn}是∂-数列,则{an}也是∂-数列.
(2)若数列{an},{bn}都是∂-数列,则{anbn}也是∂-数列.
求证:
(1)设Sn是数列{an}的前n项和,若{Sn}是∂-数列,则{an}也是∂-数列.
(2)若数列{an},{bn}都是∂-数列,则{anbn}也是∂-数列.
分析:(1)根据{Sn}为∂-数列,可得存在M>0,使|an|+|an-1|+…+|a2|≤M,利用|an+1-an|+|an-an-1|+…+|a2-a1|≤|an|+2|an-1|+…+2|a2|+|a1|≤2M+|a1|,即可证得结论.
(2)利用数列{an}{bn}都是∂-数列,可得不等式,从而可以证明|ai|<|a1|+M=M1,|bi|<|b1|+M'=M1',进而可证得结论.
(2)利用数列{an}{bn}都是∂-数列,可得不等式,从而可以证明|ai|<|a1|+M=M1,|bi|<|b1|+M'=M1',进而可证得结论.
解答:证明:(1)∵{Sn}为∂-数列,∴存在M>0,使|Sn+1-Sn|+|Sn-Sn-1|+…+|S2-S1|≤M
∴|an|+|an-1|+…+|a2|≤M,
又|an+1-an|+|an-an-1|+…+|a2-a1|≤|an|+2|an-1|+…+2|a2|+|a1|≤2M+|a1|.
∴{an}也是∂-数列.
(2)∵数列{an}{bn}都是∂-数列,∴存在M,M'使得:|an+1-an|+|an-an-1|+…+|a2-a1|≤M,|bn+1-bn|+|bn-bn-1|+…+|b2-b1|≤M′对任意n∈N都成立.
考虑|ai+1bi+1-aibi|=|ai+1(bi+1-bi)+bi(ai+1-ai)|≤|ai+1||bi+1-bi|+|bi||ai+1-ai||ai-a1|
=|(ai-ai-1)+(ai-1-ai-2)+…+(a2-a1)|≤|ai-ai-1|+|ai-1-ai-2|+…+|a2-a1|<M
∴|ai|<|a1|+M=M1
同理,|bi|<|b1|+M'=M1'
∴|ai+1bi+1-aibi|≤M1
|bi+1-bi|+M′1
|ai+1-ai|<M1M′+M1′M
∴{anbn}也是∂-数列.
∴|an|+|an-1|+…+|a2|≤M,
又|an+1-an|+|an-an-1|+…+|a2-a1|≤|an|+2|an-1|+…+2|a2|+|a1|≤2M+|a1|.
∴{an}也是∂-数列.
(2)∵数列{an}{bn}都是∂-数列,∴存在M,M'使得:|an+1-an|+|an-an-1|+…+|a2-a1|≤M,|bn+1-bn|+|bn-bn-1|+…+|b2-b1|≤M′对任意n∈N都成立.
考虑|ai+1bi+1-aibi|=|ai+1(bi+1-bi)+bi(ai+1-ai)|≤|ai+1||bi+1-bi|+|bi||ai+1-ai||ai-a1|
=|(ai-ai-1)+(ai-1-ai-2)+…+(a2-a1)|≤|ai-ai-1|+|ai-1-ai-2|+…+|a2-a1|<M
∴|ai|<|a1|+M=M1
同理,|bi|<|b1|+M'=M1'
∴|ai+1bi+1-aibi|≤M1
| n |
 |
| i=1 |
| n |
 |
| i=1 |
∴{anbn}也是∂-数列.
点评:本题考查新定义,考查放缩法的运用,解题的关键是正确理解新定义,恰当放缩,属于中档题.

练习册系列答案
相关题目
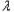 n},若存在常数M>0,对任意n∈N+,恒有|
n},若存在常数M>0,对任意n∈N+,恒有|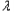 n+1﹣
n+1﹣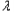 n|+|
n|+|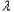 n﹣
n﹣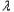 n﹣1|+…
n﹣1|+…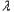 2﹣
2﹣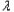 1|≤M,则称数列{
1|≤M,则称数列{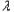 n}为
n}为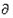 ﹣数列.
﹣数列.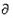 ﹣数列,则{an}也是
﹣数列,则{an}也是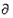 ﹣数列.
﹣数列.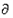 ﹣数列,则{anbn}也是
﹣数列,则{anbn}也是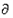 ﹣数列.
﹣数列.