题目内容
函数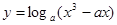 (
(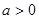 且
且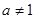 )在
)在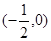 内单调递增,则
内单调递增,则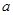 的范围是
的范围是
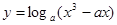 (
(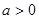 且
且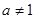 )在
)在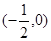 内单调递增,则
内单调递增,则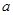 的范围是
的范围是A. | B. | C.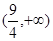 | D. |
B
试题分析:易知函数的定义域为
 ,令
,令 ,
, ,又易知函数
,又易知函数 ,所以要满足函数
,所以要满足函数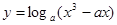 (
(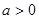 且
且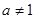 )在
)在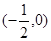 内单调递增,需
内单调递增,需 。
。点评:此题主要考查复合函数单调性的判断。判断复合函数单调性的原则是:同增异减。属于中档题。

练习册系列答案
相关题目
题目内容
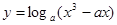 (
(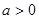 且
且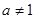 )在
)在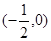 内单调递增,则
内单调递增,则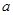 的范围是
的范围是A. | B. | C.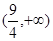 | D. |
 ,令
,令 ,
, ,又易知函数
,又易知函数 ,所以要满足函数
,所以要满足函数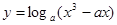 (
(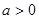 且
且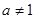 )在
)在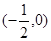 内单调递增,需
内单调递增,需 。
。