题目内容
定义在R上的函数 ,当
,当 时,
时, ,且满足下列条件:
,且满足下列条件:
① ②
② , ③
, ③ .则
.则 等于
等于
 ,当
,当 时,
时, ,且满足下列条件:
,且满足下列条件:①
 ②
② , ③
, ③ .则
.则 等于
等于A. | B. | C. | D. |
B
函数f(x)在[0,1]上是单调增函数,∵①f(1)=1,②
令x=
得,f(0)=0,令x=0,f( )=
)= ,
,
∵2f(x)=f(5x),∴f( )=
)= f(x)
f(x)
所以f( )=
)= f(1)=
f(1)= f(
f( )=
)= f(
f( )=
)= ,以此类推
,以此类推
f( )=
)= ,f(
,f( )=
)= ,f(
,f( )=
)= ,
,
再用 f( )=
)= f(x) 得,
f(x) 得,
f( )=
)= f(
f( )=
)= ,f(
,f( )=
)= f(
f( )=
)= ,f(
,f( )=
)= ,f(
,f( )=
)= ,
,
当0≤x1<x2≤1时,f(x1)≤f(x2),
而 ≤
≤ ≤
≤ ,∴f(
,∴f( )≤f(
)≤f( )≤f(
)≤f( ),
),
 ≤f(
≤f( )≤
)≤
所以,f( )=
)=
故选B.

令x=

得,f(0)=0,令x=0,f(
 )=
)= ,
,∵2f(x)=f(5x),∴f(
 )=
)= f(x)
f(x)所以f(
 )=
)= f(1)=
f(1)= f(
f( )=
)= f(
f( )=
)= ,以此类推
,以此类推f(
 )=
)= ,f(
,f( )=
)= ,f(
,f( )=
)= ,
,再用 f(
 )=
)= f(x) 得,
f(x) 得,f(
 )=
)= f(
f( )=
)= ,f(
,f( )=
)= f(
f( )=
)= ,f(
,f( )=
)= ,f(
,f( )=
)= ,
,当0≤x1<x2≤1时,f(x1)≤f(x2),
而
 ≤
≤ ≤
≤ ,∴f(
,∴f( )≤f(
)≤f( )≤f(
)≤f( ),
), ≤f(
≤f( )≤
)≤
所以,f(
 )=
)=
故选B.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 , 若方程
, 若方程 有且只有一个实根,则实数
有且只有一个实根,则实数 满足
满足



 其中t为常数.
其中t为常数. ,都有
,都有 成立,求t的取值范围;
成立,求t的取值范围; ,都有
,都有 成立,求t的取值范围.
成立,求t的取值范围. 是定义在
是定义在 上的函数,且对于任意的
上的函数,且对于任意的 ,有
,有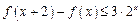 ,
, ,若
,若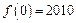 ,则
,则 ( )
( ) .
.
 .
.
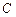 .
.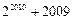
 .
.
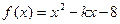 在[5,8]上是单调函数,则实数
在[5,8]上是单调函数,则实数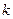 的取值范围是_____________
的取值范围是_____________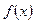 的导函数为
的导函数为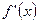 ,且满足
,且满足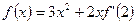 ,则
,则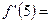 .
. ,则
,则 的值是
的值是  则不等式
则不等式 的解集是( )
的解集是( )


