题目内容
如图在长方体ABCD-A1B1C1D1中，AB=AA1=2，BC=1，点E、F、G分别是AA1、AB、DD1的中点．（I）求证：FG∥平面BCD1；
（II）求二面角A-CE-D的正弦值．
分析：（I）过G作GM∥CD交CC1于M，交D1C于O，连接BO，可得O为D1C的中点，所以GO
DC
BF，可得GF∥BO，再根据线面平行的判定定理证明线面平行．
（II）过A作AH⊥DE于H，过H作HN⊥EC于N，连接AN，由题意可得AH⊥并且AN⊥EC，可得∠ANH为二面角A-CE-D的平面角，再利用解三角形的有关知识求出答案即可．
| ||
. |
| 1 |
| 2 |
| ||
. |
（II）过A作AH⊥DE于H，过H作HN⊥EC于N，连接AN，由题意可得AH⊥并且AN⊥EC，可得∠ANH为二面角A-CE-D的平面角，再利用解三角形的有关知识求出答案即可．
解答：解：（I）过G作GM∥CD交CC1于M，交D1C于O，连接BO．
∵G为DD1的中点，∴O为D1C的中点
从而GO
DC
BF
故四边形GFBO为平行四边形…（3分）
∴GF∥BO
又GF?平面BCD1，BO?平面BCD1
∴GF∥平面BCD1． …（5分）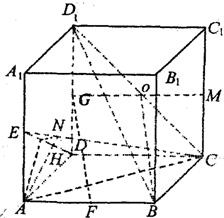
（II）过A作AH⊥DE于H，过H作HN⊥EC于N，连接AN．
∵DC⊥平面ADD1A1，
∴CD⊥AH．
又∵AH⊥DE，
∴AH⊥平面ECD．
∴AH⊥EC． …（7分）
又HN⊥EC
∴EC⊥平面AHN．
故AN⊥CE，
∴∠ANH为二面角A-CE-D的平面角 …（9分）
在Rt△EAD中，∵AD=AE=1，∴AH=
在Rt△EAC中，∵EA=1，AC=
，∴AN=
∴sin∠ANH=
=
…（12分）
∵G为DD1的中点，∴O为D1C的中点
从而GO
| ||
. |
| 1 |
| 2 |
| ||
. |
故四边形GFBO为平行四边形…（3分）
∴GF∥BO
又GF?平面BCD1，BO?平面BCD1
∴GF∥平面BCD1． …（5分）
（II）过A作AH⊥DE于H，过H作HN⊥EC于N，连接AN．
∵DC⊥平面ADD1A1，
∴CD⊥AH．
又∵AH⊥DE，
∴AH⊥平面ECD．
∴AH⊥EC． …（7分）
又HN⊥EC
∴EC⊥平面AHN．
故AN⊥CE，
∴∠ANH为二面角A-CE-D的平面角 …（9分）
在Rt△EAD中，∵AD=AE=1，∴AH=
| ||
| 2 |
在Rt△EAC中，∵EA=1，AC=
| 5 |
| ||
| 6 |
∴sin∠ANH=
| AH |
| AN |
| ||
| 5 |
点评：本小题主要考查空间线面的关系以及二面角的平面角，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力．
练习册系列答案
相关题目
6、如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为（ ）
如图在长方体ABCD-A1B1C1D1中，其中AB=BC，E，F分别是AB1，BC1的中点，则以下结论中
如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为：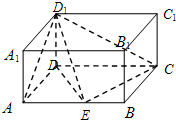
如图在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E是棱AB上的动点．
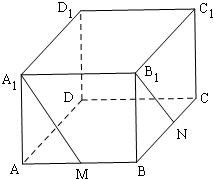如图在长方体ABCD-A1B1C1D1中，AB=a，AD=b，AC1=c，点M为AB的中点，点N为BC的中点．