题目内容
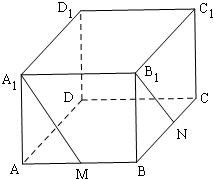如图在长方体ABCD-A1B1C1D1中，AB=a，AD=b，AC1=c，点M为AB的中点，点N为BC的中点．（1）求长方体ABCD-A1B1C1D1的体积；
（2）若a=4，b=2，c=
| 21 |
分析：（1）由勾股定理可得AC=
，进而可得CC1=
，代入体积公式可得；
（2）取AD的中点E，连A1E、EM，可证∠EA1M等于异面直线A1M与B1N所成的角或其补角，由余弦定理可得其余弦值，由反三角函数可得．
| a2+b2 |
| c2-a2-b2 |
（2）取AD的中点E，连A1E、EM，可证∠EA1M等于异面直线A1M与B1N所成的角或其补角，由余弦定理可得其余弦值，由反三角函数可得．
解答：
解：（1）连AC、AC1，∵△ABC是直角三角形，∴AC=
．
∵ABCD-A1B1C1D1是长方体，∴C1C⊥BC，C1C⊥CD，
又DC∩BC=C，∴C1C⊥平面ABCD，∴C1C⊥AC．
又在Rt△ACC1中，AC1=c，AC=
，∴CC1=
，
∴VABCD-A1B1C1D1=ab
（2）取AD的中点E，连A1E、EM，
∵EN
AB
A1B1，∴四边形A1B1NE为平行四边形，
∴A1E∥B1N，∴∠EA1M等于异面直线A1M与B1N所成的角或其补角．
∵AM=2，AE=1，AA1=1，得A1M=
，A1E=
，EM=
，
∴cos∠EA1M=
=
，∠EA1M=arccos
．
∴异面直线A1M与B1N所成的角等于arccos
解：（1）连AC、AC1，∵△ABC是直角三角形，∴AC=| a2+b2 |
∵ABCD-A1B1C1D1是长方体，∴C1C⊥BC，C1C⊥CD，
又DC∩BC=C，∴C1C⊥平面ABCD，∴C1C⊥AC．
又在Rt△ACC1中，AC1=c，AC=
| a2+b2 |
| c2-a2-b2 |
∴VABCD-A1B1C1D1=ab
| c2-a2-b2 |
（2）取AD的中点E，连A1E、EM，
∵EN
| ||
. |
| ||
. |
∴A1E∥B1N，∴∠EA1M等于异面直线A1M与B1N所成的角或其补角．
∵AM=2，AE=1，AA1=1，得A1M=
| 5 |
| 2 |
| 5 |
∴cos∠EA1M=
| ||
2•
|
| ||
| 10 |
| ||
| 10 |
∴异面直线A1M与B1N所成的角等于arccos
| ||
| 10 |
点评：本题考查长方体的体积公式，以及异面直线所成的角，属中档题．
练习册系列答案
相关题目
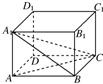6、如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为（ ）
如图在长方体ABCD-A1B1C1D1中，其中AB=BC，E，F分别是AB1，BC1的中点，则以下结论中
如图在长方体ABCD-A1B1C1D1中，三棱锥A1-ABC的面是直角三角形的个数为：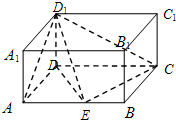
如图在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E是棱AB上的动点．