题目内容

已知x∈R，求证：ex≥x+1.

思路分析：首先应构造函数，对函数进行求导，并判断函数的单调性.?

证明：令f（x）=ex-x-1，

∴f′（x）=ex-1.

∵x∈［0，+∞），∴ex-1≥0恒成立，即f′（x）≥0.

∴f（x）为增函数，当x∈（-∞，0）时，f′（x）=ex-1＜0，?

∴f（x）是减函数.

又∵f（0）=0，

∴当x∈R时f（x）≥f（0）.?

即ex-x-1≥0.

∴ex≥x+1.

温馨提示

实质是判断函数的单调性.

练习册系列答案
相关题目
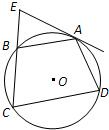
精英家教网附加题：
A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
求证：AB2=BE•CD．
B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
an+4
bn+4
=M
an
bn
，试求二阶矩阵M．
C．已知椭圆C的极坐标方程为ρ2=
12
3cos2θ+4sin2θ
，点F1，F2为其左、右焦点，直线l的参数方程为
x=2+
2
2
t
y=
2
2
t
（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
D．已知x，y，z均为正数．求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．
已知a∈R，函数f(x)=
ax
+lnx-1，g（x）=（lnx-1）ex+x（其中e为自然对数的底数）．
（1）讨论函数f（x）在（0，e]上的单调性；
（2）是否存在实数x0∈（0，+∞），使曲线y=g（x）在点x=x0处的切线与y轴垂直？若存在，求出x0的值；若不存在，请说明理由．
（3）若实数m，n满足m＞0，n＞0，求证：nnem≥mnen．
已知a∈R，函数f(x)=
a
x
+lnx-1，g（x）=（lnx-1）ex+x．
（1）求函数f（x）在区间（0，e]上的最小值；
（2）是否存在实数x0∈（0，e]，使曲线y=g（x）在点x=x0处的切线与y轴垂直？若存在，求出x0的值，若不存在，请说明理由；
（3）求证：(1+
1
2
+
1
3
+…+
1
n
)•
n
k=1
ln[k(k+1)(k+2)]＞(n-
1
4
)•ln
en
n!
      (n∈N*)．
（2013•大连一模）已知m∈R，函数f（x）=mx2-2ex．
（Ⅰ）当m=2时，求函数f（x）的单调区间；
（Ⅱ）若f（x）有两极值点a，b（a＜b），（ⅰ）求m的取值范围；（ⅱ）求证：-e＜f（a）＜-2．
A．如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．
B．已知矩阵A=
.
1-2
3-7
.
．
（1）求逆矩阵A-1；
（2）若矩阵X满足AX=
3
1
，试求矩阵X．
C．坐标系与参数方程
已知极坐标系的极点O与直角坐标系的原点重合，极轴与x轴的正半轴重合，曲线C1：ρcos（θ+
π
4
）=2
2
与曲线C2：
x=4t2
y=4t
，（t∈R）交于A、B两点．求证：OA⊥OB．
D．已知x，y，z均为正数，求证：
x
yz
+
y
zx
+
z
xy
≥
1
x
+
1
y
+
1
z
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网