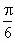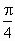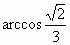题目内容
(2007
北京西城模拟)设集合W是满足下列两个条件的无穷数列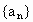 的集合:
的集合:
①
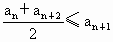 ;②
;②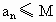 ,其中
,其中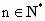 ,M是与n无关的常数.
,M是与n无关的常数.
(1)
若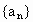 是等差数列,
是等差数列,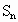 是其前n项的和,
是其前n项的和, ,
,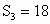 .
.
证明:
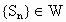 ;
;
(2)
设数列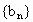 的通项为
的通项为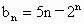 ,且
,且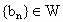 .求M的取值范围;
.求M的取值范围;
(3)
设数列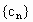 的各项均为正整数,且
的各项均为正整数,且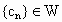 .
.
证明:
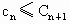 .
.
答案:略
解析:
解析:
|
解析: (1)设等差数列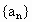 的公差是d,则 的公差是d,则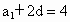 , ,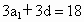 , ,
解得 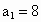 ,d=-2.所以 ,d=-2.所以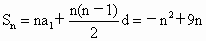 .由 .由
得 又 所以当n=4或5时, (2) 因为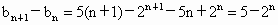 . .
所以当 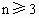 时, 时,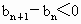 ,此时数列 ,此时数列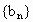 单调递减; 单调递减;
当 n=1,2时,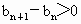 , ,
即 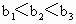 , ,
因此数列 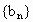 中的最大项是 中的最大项是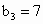 , ,
所以 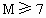 . .
(3) 假设存在正整数k,使得 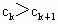 成立. 成立.
由数列 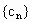 的各项均为正整数,可得 的各项均为正整数,可得 ,即 ,即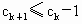 . .
因为 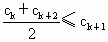 , ,
所以 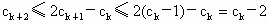 . .
由 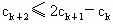 及 及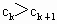 , ,
得 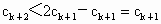 , ,
故 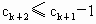 . .
因为  , ,
所以 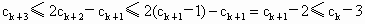 .… .…
依此类推,可得 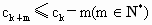 . .
设 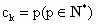 ,则当m=P时,有 ,则当m=P时,有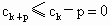 , ,
这显然与数列 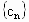 的各项均为正整数矛盾! 的各项均为正整数矛盾!
所以假设不成立,即对于任意 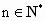 ,都有 ,都有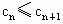 成立. 成立. |

练习册系列答案
相关题目
(2007
北京西城模拟)在1,2,3,4,5这五个数字所组成的没有重复数字的三位数中,其各个数字之和为9的三位数共有[
]|
A .16个 |
B .18个 |
C .19个 |
D .21个 |
(2007
北京西城模拟)若集合 ,
, 满足
满足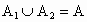 ,则记[
,则记[ ,
,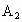 ]是A的一组双子集拆分.规定:[
]是A的一组双子集拆分.规定:[ ,
,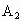 ]和[
]和[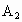 ,
,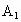 ]是A的同一组双子集拆分.已知集合A={1,2,3},那么A的不同双子集拆分共有
]是A的同一组双子集拆分.已知集合A={1,2,3},那么A的不同双子集拆分共有
[
]|
A .15组 |
B .14组 |
C .13组 |
D .12组 |
(2007
北京西城模拟)已知函数y=sin wx在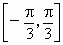 上是减函数,则w的取值范围是
上是减函数,则w的取值范围是
[
]|
A .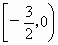 |
B .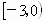 |
C .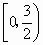 |
D .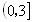 |
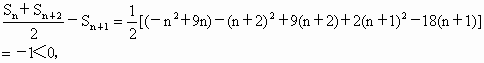
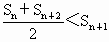 ,适合条件①;
,适合条件①;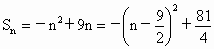 ,
,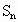 取得最大值20,即
取得最大值20,即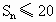 ,适合条件②.综上,
,适合条件②.综上,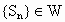 .
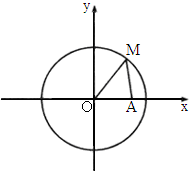
.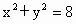 ,动点M在圆O上,那么∠OMA的最大值是
,动点M在圆O上,那么∠OMA的最大值是