题目内容
已知数列 的前
的前 项和
项和 。
。
(1)求数列的通项公式;
(2)求 的最大或最小值.
的最大或最小值.
 的前
的前 项和
项和 。
。(1)求数列的通项公式;
(2)求
 的最大或最小值.
的最大或最小值.(1)  (2)
(2)  或
或 ,此时
,此时 有最小值
有最小值 ,无最大值.
,无最大值.
 (2)
(2)  或
或 ,此时
,此时 有最小值
有最小值 ,无最大值.
,无最大值.试题分析:(1) 根据已知
 求
求 ,可知利用
,可知利用 ,求出
,求出 和
和 ,而后验证是否可以合为一个通项公式.
,而后验证是否可以合为一个通项公式.(2)根据
 可知,其是一个开口向上的二次函数,其中
可知,其是一个开口向上的二次函数,其中 .所以其无最大值,有最小值在对称轴处取得,即
.所以其无最大值,有最小值在对称轴处取得,即 时.但是显然
时.但是显然 ,所以取离它最近的整数
,所以取离它最近的整数 的值,从而得到
的值,从而得到 的最小值.
的最小值.(1)当
 时,
时, ,
,当
 时,
时, ,
,验证将
 带入
带入 时的
时的 中可得
中可得 ,不成立,
,不成立,所以数列的通项公式
 .
.(2)根据
 可知,其是一个开口向上的二次函数,其中
可知,其是一个开口向上的二次函数,其中 .
.所以
 无最大值,有最小值在对称轴处取得,即
无最大值,有最小值在对称轴处取得,即 时,
时,显然此时
 ,所以取离它最近的正整数
,所以取离它最近的正整数 的值,
的值,即
 或
或 ,此时
,此时 有最小值
有最小值 .
. 求
求 ,可知利用
,可知利用 ;将数列前
;将数列前 项和当做二次函数求最值.
项和当做二次函数求最值.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, .
. ;
; ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 满足
满足 ,且
,且 .
. 的值;
的值;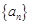 是等比数列, 且
是等比数列, 且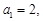
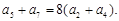 数列
数列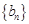 满足:对任意正整数
满足:对任意正整数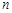 ,有
,有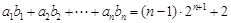 .
. 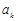 与
与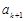 之间插入
之间插入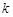 个
个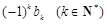 后,得到一个新的数列
后,得到一个新的数列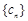 . 求数列
. 求数列 满足:
满足: ,
, ,
, ,那么使
,那么使 成立的
成立的 的最大值为( )
的最大值为( )  试写出
试写出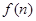 的表达式;
的表达式; 中,已知
中,已知 ,则
,则 = ( ).
= ( ).