题目内容
已知椭圆
的离心率为
，过右顶点A的直线l与椭圆C相交于A、B两点，且
．
（1）求椭圆C和直线l的方程；
（2）记曲线C在直线l下方的部分与线段AB所围成的平面区域（含边界）为 D．若曲线
与D有公共点，试求实数m的最小值．
解:（1）由离心率
，得
，即
． ① ……2分
又点在椭圆
上，即
． ② ……4分
解 ①②得
，故所求椭圆方程为
． ……5分
由
得直线l的方程为
．………6分
（2）曲线，即圆
，其圆心坐标为
，半径
，表示圆心在直线
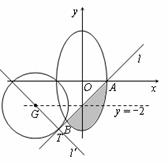
上，半径为
的动圆．由于要求实数m的最小值，由图可知，只须考虑
的情形．
设
与直线l相切于点T，则由
，得
，………… 10分
当
时，过点
与直线l垂直的直线
的方程为
，解方程组
得
．……………… 12分
因为区域D内的点的横坐标的最小值与最大值分别为
，所以切点
，由图可知当过点B时，m取得最小值，即
，解得
．……… 14分
练习册系列答案
阅读快车系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：