题目内容
已知数列{an}为公差大于0的等差数列,Sn为其前n项和,且a1a6=21,S6=66.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=xan+3,求{bn}的前n项和Tn;
(3)若数列{cn}是等差数列,且cn=
,求常数p.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=xan+3,求{bn}的前n项和Tn;
(3)若数列{cn}是等差数列,且cn=
| Sn | n+p |
分析:(1)由 S6=66 求出a1+a6=22,再由a1a6=21,公差大于0可得 a1=1,a6=21,求出公差d=4,可得数列{an}的通项公式.
(2)先求出bn=xan+3=x4n+9,分x=0时、x=1时、x≠0 且x≠-1时三种情况,分别求得,{bn}的前n项和 Tn的值,
综合可得结论.
(3)先求出 Sn=2n2-n,可得cn=
=
.再由c1+c3=2c2,由此解得 p的值.
(2)先求出bn=xan+3=x4n+9,分x=0时、x=1时、x≠0 且x≠-1时三种情况,分别求得,{bn}的前n项和 Tn的值,
综合可得结论.
(3)先求出 Sn=2n2-n,可得cn=
| Sn |
| n+p |
| 2n2-n |
| n+p |
解答:解:(1)∵S6=66=
,∴a1+a6=22.再由a1a6=21
可得 a1 和a6是方程 x2-22x+21=0的两个根,再由公差大于0可得 a1=1,a6=21,
由于a6=21=a1+5d,故公差d=4,故 an =4n-3.
(2)bn=xan+3=x4n+9,
当x=0时,bn=xan+3=0,{bn}的前n项和 Tn=0.
当x=1时,bn=xan+3=1,{bn}的前n项和 Tn=n.
当x=-1时,bn=xan+3=-1,{bn}的前n项和Tn=-n.
当x≠0 且x≠±1时,bn=x4n+9,{bn}的前n项和 Tn=
.
综合可得,{bn}的前n项和Tn=
.
(3)∵Sn=n×1+
×4=2n2-n,∴cn=
=
.
∵{cn}是等差数列,∴c1+c3=2c2,即
+
=2×
,
由此解得 p=0,或 p=-
.
| 6(a1+a6) |
| 2 |
可得 a1 和a6是方程 x2-22x+21=0的两个根,再由公差大于0可得 a1=1,a6=21,
由于a6=21=a1+5d,故公差d=4,故 an =4n-3.
(2)bn=xan+3=x4n+9,
当x=0时,bn=xan+3=0,{bn}的前n项和 Tn=0.
当x=1时,bn=xan+3=1,{bn}的前n项和 Tn=n.
当x=-1时,bn=xan+3=-1,{bn}的前n项和Tn=-n.
当x≠0 且x≠±1时,bn=x4n+9,{bn}的前n项和 Tn=
| x13(1-x4n) |
| 1-x4 |
综合可得,{bn}的前n项和Tn=
|
(3)∵Sn=n×1+
| n(n-1) |
| 2 |
| Sn |
| n+p |
| 2n2-n |
| n+p |
∵{cn}是等差数列,∴c1+c3=2c2,即
| 1 |
| 1+p |
| 15 |
| 3+p |
| 6 |
| 2+p |
由此解得 p=0,或 p=-
| 1 |
| 2 |
点评:本题主要考查等差关系的确定,等差数列的定义和性质,等差数列的通项公式,前n项和公式的应用,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
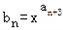 ,求{bn}的前n项和Tn;
,求{bn}的前n项和Tn;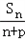 ,求常数p.
,求常数p.