题目内容
已知正项数列 ,
, ,且
,且
(1)求证: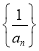 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)数列 满足
满足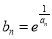 ,若
,若 ,仍是
,仍是 中的项,求
中的项,求 在区间
在区间 中的所有可能值之和
中的所有可能值之和 ;
;
(3)若将上述递推关系 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数 的取值范围
的取值范围
【解析】
(1)对 两边取倒数,得
两边取倒数,得 ,故
,故 是等差数列,
是等差数列,
又 ,故
,故
(2)
设 是
是 中的第
中的第 项,则
项,则 ,
,
所以
(3)对 两边取倒数,得
两边取倒数,得 ,
,

 ,而
,而 ,所以
,所以
【解析】
试题分析(1)对 两边取倒数,证明
两边取倒数,证明 是等差数列;(2)化简等比数列前n项积,再用通项列方程;(3)对
是等差数列;(2)化简等比数列前n项积,再用通项列方程;(3)对 两边取倒数,用裂项法化简。
两边取倒数,用裂项法化简。
考点;数列的综合.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象向左平移
的图象向左平移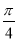 个单位,再向上平移1个单位,所得图象的函数解析式是( )
个单位,再向上平移1个单位,所得图象的函数解析式是( )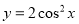 (B)
(B)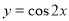
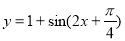 (D)
(D)
 =
= .将函数
.将函数 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是( )
个单位,以下是所得函数图象的一个对称中心是( ) B.
B. C.
C. D.
D.
 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图像关于点
的图像关于点 对称,
对称, 、
、 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的
的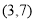 B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则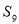 等于
等于 B.
B. C.
C. D.
D.
 表示二进制的数,将它转换成二进制的形式是
表示二进制的数,将它转换成二进制的形式是 ,那么将二进制数
,那么将二进制数 转换成十进制的形式是( )
转换成十进制的形式是( ) B.
B. C.
C. D.
D.
 ,
, ,则使不等式
,则使不等式 成立的最大自然数
成立的最大自然数 为____________
为____________