题目内容
已知函数![]() 的图象为曲线
的图象为曲线![]() .
.
(I)若曲线![]() 上存在点
上存在点![]() ,使曲线
,使曲线![]() 在
在![]() 点处的切线与
点处的切线与![]() 轴平行,求
轴平行,求![]() 的关系;
的关系;
(II)说明函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,并求此时
时取得极值,并求此时![]() 的值;
的值;
(III)在满足(2)的条件下,![]() 在
在![]() 时恒成立,求
时恒成立,求![]() 的取值范围.
的取值范围.
解:(1)![]() ,设切点为
,设切点为![]() ,
,
则曲线![]() 在点P的切线的斜率
在点P的切线的斜率![]() ,
,
由题意知![]() 有解,
有解,
∴![]() 即
即![]() .
.
(2)若函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,
时取得极值,
则![]() 有两个解
有两个解![]() 和
和![]() ,且满足
,且满足![]() .
.
易得![]() .
.
(3)由(2),得![]() .
.
根据题意,![]() (
(![]() )恒成立.
)恒成立.
∵函数![]() (
(![]() )在
)在![]() 时有极大值
时有极大值![]() (用求导的方法),
(用求导的方法),
且![]()
![]() ,
,![]() .
.
∴函数![]() (
(![]() )的最大值为
)的最大值为![]() .所以
.所以![]() .
.

练习册系列答案
相关题目
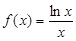 的图象为曲线
的图象为曲线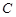 , 函数
, 函数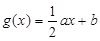 的图象为直线
的图象为直线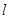 .
.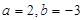 时, 求
时, 求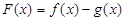 的最大值;
的最大值;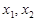 , 且
, 且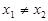 ,
,  .
. 的图象为曲线C。
的图象为曲线C。 轴平行,求
轴平行,求 的关系;
的关系; 时取得极值,求此时
时取得极值,求此时 的取值范围。
的取值范围。