题目内容
(本题满分16分) 本题共有3个小题,第1小题满分7分,第2小题满分7分,第3小题满分2分.
设直线 交椭圆
交椭圆 于
于 两点,交直线
两点,交直线 于点
于点 .
.
(1)若 为
为 的中点,求证:
的中点,求证: ;
;
(2)写出上述命题的逆命题并证明此逆命题为真;
(3)请你类比椭圆中(1)、(2)的结论,写出双曲线中类似性质的结论(不必证明).
【答案】
(1)设
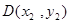
 ,
,
 ,
,

又


(2)逆命题:设直线 交椭圆
交椭圆 于
于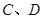 两点,交直线
两点,交直线 于点
于点 .若
.若 ,则
,则 为
为 的中点.
的中点.
证明:由方程组
因为直线 交椭圆
交椭圆 于
于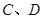 两点,
两点,
所以 ,即
,即 ,设
,设 、
、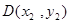 、
、
则 ,
,
 又因为
又因为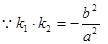 ,所以
,所以
 ,故E为CD的中点.
,故E为CD的中点.
(3) 为
为 中点的充要条件是
中点的充要条件是 .
.
【解析】
试题分析:(1)解法一:设
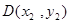


 ,
,

又


解法二(点差法):设
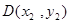

 ,
,
两式相减得
即


(2)逆命题:设直线 交椭圆
交椭圆 于
于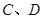 两点,交直线
两点,交直线 于点
于点 .若
.若 ,则
,则 为
为 的中点.
的中点.
证法一:由方程组
因为直线 交椭圆
交椭圆 于
于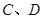 两点,
两点,
所以 ,即
,即 ,设
,设 、
、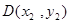 、
、
则 ,
,
 又因为
又因为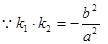 ,所以
,所以
 ,故E为CD的中点.
,故E为CD的中点.
证法二:设
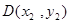

则 ,
,
两式相减得
即
又 ,
, 即
即

得
 ,即
,即 为
为 的中点.
的中点.
(3)设直线 交双曲线
交双曲线 于
于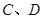 两点,交直线
两点,交直线 于点
于点 .则
.则 为
为 中点的充要条件是
中点的充要条件是 .
.
考点:本题考查了直线与圆锥曲线的位置关系
点评:求过定点的圆锥曲线的中点弦问题,通常有下面两种方法:(1)点差法,即设出弦的两端点的坐标代入圆锥曲线方程后相减,得到弦中点坐标与弦所在直线斜率的关系,从而求出直线方程.(2)联立法,即将直线方程与双曲线方程联立,利用韦达定理与判别式求解.

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在